アクチュアリー試験の一次試験の科目の一つである「年金数理」。
他の一次試験の科目に比べると、年金数理に登場する数理的手法は複雑ではありません。にもかかわらず、難関科目の一つに位置付けられている、その理由は、
「実務経験がないので、教科書や問題文の意味がわからない」
これが一番ではないでしょうか。
勉強するときに、教科書がスラスラ読めると学習は進みます。でも、逆もしかり。教科書を読んでいて、意味が分からない単語が登場したり、理解できない論理展開が登場すると、そっと教科書を閉じる。そんな繰り返しをした受験生も多いと思います。
本サイトは、そんな受験生をサポートする目的で作られたものです。
年金数理の過去の合格率の推移は以下のとおり。かなり凸凹していることがわかります。
ビッグウェーブに乗り遅れて苦労している、そんな受験生の声を聞くことも少なくありません。
「合理的な努力をした学生が合格できる」
アクチュアリー試験は、そんな試験であってほしいと思っています。年金数理の試験と教科書のギャップを埋める、その一助になれば幸いです。
年金数理とは何か
「年金数理(平成27年3月改訂版)」(以下、単に教科書と呼ぶ)の冒頭に、年金制度の分類が載っていますが、それを補足すると…
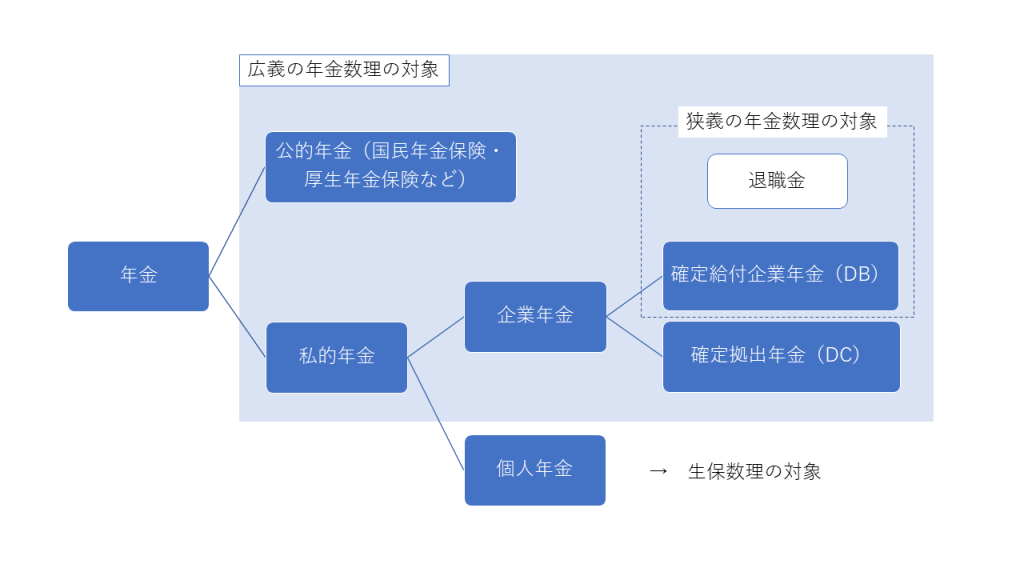
- 教科書では、年金数理の対象を「広義」の意味で記載していますが、日本の大半の年金アクチュアリー(試験委員を含む)は「狭義」の世界で働いています。
- したがって、必然的に年金数理の試験問題は「狭義の年金数理」が対象となります。
- 「年金」と言えば公的年金を想像すると思います。その正式名称は「国民年金保険」「厚生年金保険」というように、「保険」という単語もついています。公的年金の方が企業年金よりも、保険の機能が強いことを示唆しています。
- 退職金と企業年金は切っても切れない関係にあります。退職金は年金制度とは異なりますが、従業員の退職をトリガーに給付を行うという意味では共通しています。退職金と企業年金を総称して、退職給付制度と呼ぶこともあります。
- 教科書では、厚生年金基金・確定給付企業年金というように、法令上の名称を記載していますが、年金数理において「厚生年金基金とは何か」を学ぶことは不要です。
- 米国では、DCも年金数理の対象としています(参照:Actuarial Mathematics for Life Contingent Risksの第9章)が、日本の試験においては、DBとDCの違いを理解しておけば十分です。
- 教科書にも記載があるように、「個人年金」は生保数理の対象ですが、その一部の手法は被っています。教科書の第1章と第2章の多くは、生保数理の内容と重複しています。生保数理と年金数理をセットで受験すると効率的と言われる所以は、ここにあります。
学生から見たときの公的年金
「国民年金」の保険料をちゃんと払っていますか?
講義の冒頭で、いつもこの質問を投げかけるようにしています。生保数理を勉強したことのある人であれば、営業保険料=「純保険料」+「付加保険料」であることを知っていると思います。この「付加保険料」は、保険会社の事業費を賄うための保険料。公的年金の保険料には、この「付加保険料」に相当する部分は含まれていません。このことからも、国民年金の保険料を払わず、個人年金を購入することは経済的な意味で合理的な行動ではないことが理解できると思います。
他にも、
- 公的年金の財源の一部は税金
- 公的年金には老齢給付の他に、障害給付や遺族給付などもある
- 国と保険会社の信用力の違い
など、公的年金の優位性を示すことは容易です。
また、「公的年金の方が企業年金よりも、保険の機能が強い」と記載しました。公的年金は、年金であると同時に、保険でもあります。保険ということは何かの「リスク」を保障している、ということです。具体的には、
- 長寿リスク
- 障害リスク
- (小さい子供を残したまま世帯主が死亡した場合に備える)死亡リスク
- インフレリスク
このあたりは厚労省が制作したクイズ動画を見ると、楽しく学べると思います。
退職金と企業年金は切っても切れない関係
退職金と企業年金。以下の記載から、その歴史は、退職金の方が古いことがわかります。
雇用者一般に対して、職業生活の引退にあたって金銭給付を行うという現在的な意味での退職給付は、明治期以降の近代化による給与所得者の増加に伴って発達した退職一時金制度がその最初の形であろう。当時の企業では熟練従業員定着のための労働管理上のインセンティブとして退職金制度の整備が行われ、その給付は主として定年退職時に巨額の一時金を支給する形態が採られており、老後の所得保障機能の強い年金はほとんど発達しなかった。
「海外の年金制度」の90頁(東洋経済新報社、厚生年金基金連合会編)
平成30年就労条件総合調査を見ると、退職一時金制度のみ実施している企業が59.1%と過半数を超えています。
このように退職金は歴史も古く、多くの企業が導入しています。一方、企業年金を導入している企業は20%程度。意外と少ないと感じる人もいると思います。
年金アクチュアリーの多くが所属する信託銀行や生命保険会社のパーパス(存在意義)の一つは、企業年金の普及と発展。これを言い換えると、
退職金を企業年金に移行する
ということを意味します。
ここで「移行」という言葉が登場しました。これはどういう意味でしょうか。
例えば、定年で退職すると1000万円の一時金が貰える退職金制度を考えます。この制度の100%を年金制度に移行すると、従業員は定年で退職した場合、退職金制度から貰う一時金はありません。一方で、年金制度からは「1000万円を原資として計算した年金額」をもらうことができます。この年金額の計算には、生保数理に関する知識が必要となるので後述します。
一方で、退職金の70%を移行している場合、従業員が定年退職すると、退職金制度から300万円の一時金をもらうことができます。加えて、年金制度からは「700万円を原資として計算した年金額」をもらうことができます。これが、円グラフでいうところの「両制度併用」という企業の典型例です。
この100%や70%という割合を「移行割合」と呼びます。
では、退職金を企業年金に移行すると、どんなメリットが生じるのでしょうか。
まず、従業員の視点で見ると、
- 年金で受け取ることができる。やっぱり一時金を選択、というのも可なので、受け取りの選択肢が広がる。
- 年金で受け取ると、その総額は退職一時金よりも大きくなる。
- 年金資産は、企業の外部に積み立てられるので、万が一企業が倒産しても、年金資産は従業員などのものとして確保される。
次に、企業の視点で見ると、
- 企業が年金制度に拠出する保険料(掛金)の全額を損金とすることができる。
- 退職給付にかかる資金負担が平準化できる。
といったことが、代表的な理由です。
DBとDCの違い

年金制度はキャッシュフローを交換する金融取引です。掛金と給付に着目して、DBとDCの特徴を見てみましょう。
DBの場合、Defined Benefitという名称から推察できるように、あらかじめ「給付の算定方法」が決まっています。そして、その給付を賄うための掛金を計算し、企業が掛金を拠出します。
DCの場合、あらかじめ「掛金額」が決まっています。そして、拠出した掛金と運用収益の合計額で給付が決まることになります。
DBもDCも資産運用を伴いますが、運用リスクの帰属先は異なります。資産運用に失敗した場合を考えてみましょう。DBの場合、運用差損が発生すると、その分積立不足が生じます。その積立不足を掛金で穴埋めする責任を負っているのは企業です。一方、DCの場合、運用差損が発生すると、その分給付が目減りします。したがって、DCで運用リスクを負っているのは個人ということになります。
ここで、DBはあらかじめ「給付の算定方法」が決まっているという説明を行いました。あらかじめ決まっているのは、「給付額」ではなく、「給付の算定方法」です。この「給付の算定方法」には、以下のような種類があります。
- 定額:退職時の勤続年数もしくは年齢に応じた一定の金額を定める方式
- 最終給与比例:退職時の給与に一定割合を乗じる方式
- 累積給与比例:在職期間中の給与の累積に一定割合を乗じる方式
- ポイント制:在職期間中の資格・役職に応じたポイントの累積にポイント単価を乗じたものに、一定割合を乗じる方式
- キャッシュバランスプラン(CB制度):拠出クレジットと利息クレジットの元利合計に、一定割合を乗じる方式
このような給付設計の多様性が、日本の特徴の一つと言われています。その背景には、退職金を移行して企業年金を設立している企業が多いという点があります。退職金の方が歴史が古い、という説明を行いました。退職金の給付設計がもともと多様であったので、その移行先であるDBの給付設計も多様になっている、ということです。
もう少し詳しく、具体例を用いて、個々の給付設計を見てみましょう。
| 給付の算定方法の例示 | |
| 定額 | 一時金額 = 勤続年数 × 100,000円 年金額 = 一時金額 ×(1+据置利率)n ÷ 年金現価率 |
| 最終給与比例 | 一時金額 = 脱退時の基準給与 × 勤続年数に応じた支給率 年金額 = 一時金額 ×(1+据置利率)n ÷ 年金現価率 |
| 累積給与比例 | 一時金額 = 給与累計 × 支給率 年金額 = 一時金額 ×(1+据置利率)n ÷ 年金現価率 |
| ポイント制 | 一時金額 = ポイント累計 × ポイント単価 年金額 = 一時金額 ×(1+据置利率)n ÷ 年金現価率 |
| CB制度 | 一時金額 = 仮想個人勘定残高 年金額 = 一時金額 ÷ 年金現価率 |
CB制度を除き、一時金額の計算には違和感ないと思います。ただ、年金額の計算には少し留意が必要です。「年金現価率」という用語を無定義で使っていますが、ここでは支給年数のことだと思っておいてください。例えば、支給期間が20年であれば20です。(実際は、利息を加味する分、20よりも小さい)
いずれの給付設計も、
- 一時金額の額計算する
- 一時金額をベースに年金額の計算を行う
というステップになっています。
なぜ、一時金額を経由して年金額の計算を行っているのでしょうか。その理由も、退職金を移行してDBを作っているからです。退職金は一時金ベースの退職給付制度です。それを移行するかたちでDB制度は作られるので、DBについても、最初に一時金額が決まります。年金額は、(移行した)一時金額と等価になるように設定されるので、上記のような算式となっています。
また、いずれの給付設計も「据置利率」と「給付利率」という概念が登場しています。

ここで、据置利率、給付利率は、予定利率とは別物です。据置利率と給付利率は、あくまでも給付額を計算するための率であり、予定利率は数理計算上の前提です。
学生から聞くよくある質問で、「保証期間付き終身年金」の場合の年金額の設定方法についても補足しておきます。教科書でいうと、31頁に登場するタイプの年金です。保証期間付き終身年金の場合、実務上、
一時金額=年金額×保証期間の年金現価率
として、年金額の計算を行っています。したがって、一時金額と保障期間付き終身年金は等価となりません。終身部分は、企業の持ち出し(従業員から見ると増額)と言われることもあります。
まとめると、年金額は一時金額と給付利率で等価になるように設定される(ただし、保証期間付き終身の場合は、保証期間の年金と等価)ということになります。保証期間付き終身の場合は、年金額の計算方法が問題文に明記されていると思うので、問題文を注意して読むようにしてください。
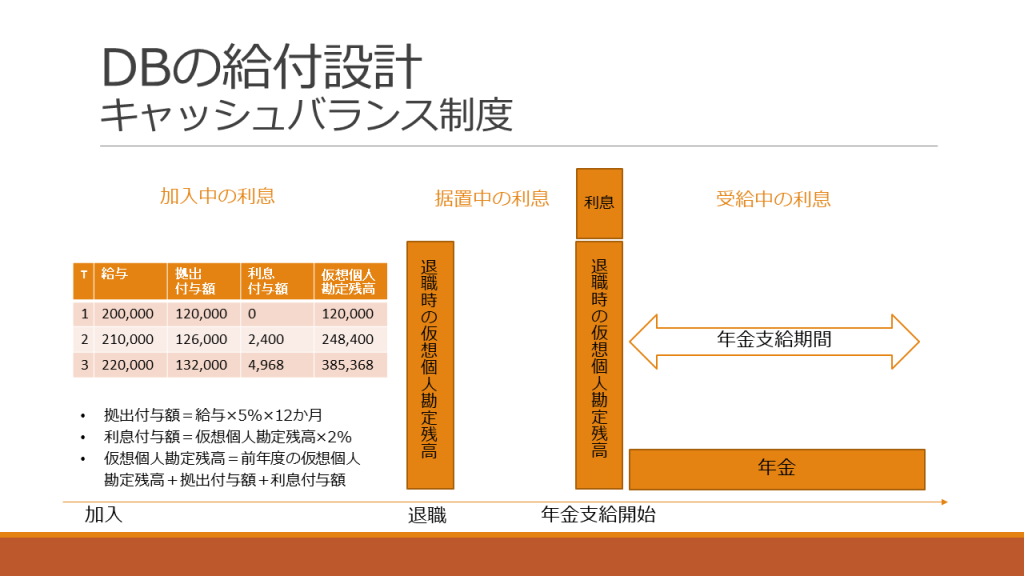
給付設計について、もう一点補足します。CB制度についてです。これも、教科書の記載は少ないが、試験には登場しやすい、受験生には有名なギャップに相当するものです。
一時金額を決める「仮想個人勘定残高」は、実務上、以下のように計算されます。CB制度の場合、加入中の利息、据置中の利息、受給中の利息がすべて変動する可能性があります。これらが予定利率とは別物である点は、既述と同様です。
生保数理と年金数理の類似点
生保数理も年金数理も、
- 将来の支払額を予測
- 将来の支払額の現在価値を求める
という点では共通しています。ここで、①は、年金制度から支払われる給付額が、いつ、そしていくら発生するかを予測することです(生保では、保険金が、いつ・いくら発生するかを予測することに対応)。給付の予測には、「計算基礎率」を用います。用いる基礎率の種類は異なりますが、計算基礎率という前提をおいて将来予測を行うという点は同じです。
そして、②は、①で計算した将来の給付額を予定利率で割り引いて合計するプロセスです。具体的には、予定利率を\(i\)、各年度の期末に支払われる給付額(厳密に言うと、その期待値)を\(A(t)(t=1,2,3,...)\)とすると、
$$ 現在価値 = \frac{A(1)}{1+i} + \frac{A(2)}{(1+i)^2} + \frac{A(3)}{(1+i)^3} + ... $$
生保数理と似た考え方ですね。
他にも、
- 大数の法則に基づく
- 収支相等の原則に基づく
- 責任準備金という、将来の支払いに備えて現時点で保有しておくべき額という概念が登場する など
類似点を探すと色々と見つかります。
生保数理と年金数理の相違点
上記で求めた現在価値は、将来の給付の総額に対応するものです。これを「給付現価」と呼びます。給付現価のすべてを現時点で用意するということも考えられますし、支払いが必要な時になってはじめて資金を準備するという考え方もあります。また、その中間的な方法もあります。このように、今から将来にわたって、どのように保険料を積み立てていくのかを「財政方式」と呼びます。この財政方式は、年金数理に特有の考え方です。
また他にも、
| 企業年金 | 生命保険 |
| 企業年金の保険料は、一般に企業が支払う(なぜなら、退職金からの移行だから) | 生命保険の保険料は契約者が支払う |
| 企業年金は、定期的に保険料を見直す前提で財政運営を行う | 生命保険の保険料が見直されることは、滅多にない |
| 企業年金は、財政上の不足が許容されるが、不足は将来の保険料で穴埋めすることになる | 生命保険の収支が悪化した場合、売り止めになる可能性がある(例:コロナ保険) |
| 企業年金に生じた剰余は企業年金に帰属し、母体企業に返還されることはない | 生命保険に生じた剰余は生命保険会社に帰属する |
| 事業費は保険料とは別に徴収する | 事業費は保険料に含めて徴収する |
ここで、よく「企業年金は集団全体で収支相等」「生命保険は個人単位で収支相等」という説明がなされることがあります。実際、教科書にも、以下のような記載があります。
特定の集団を対象として、その集団全体での収支相等を考えることが挙げられる。年金制度の保険料は多くの場合、集団全体で収支相等するよう算出された保険料率が年齢等に関係なく全員一律に適用される。言い換えれば、集団を形成する個人ごとでの収支相等は必ずしも成立しない。
教科書の3頁
この記載は、年金アクチュアリーが実務で利用している「加入年齢方式」や「開放基金方式」と呼ばれる財政方式を念頭においた記載です。年金数理の特徴は、多様な財政方式(ここでは、保険料を積み立てるペースという理解でOK)にあり、そのうち実務で採用されている財政方式について言うと、教科書3頁のような特徴がある、ということです。
年金数理の目的
年金アクチュアリーの活躍領域は、主に以下の3つです。
- 企業年金の制度設計コンサル
- 保険料の計算
- 決算
企業年金は3つのRをマネジメントするためのスキームという説明がなされることがあります。3つのRとは、採用(Recruit)、引き留め(Retention)、引退(Retirement)です。中途採用を積極的に行うのであればDCの方が適しています。一定年齢以上の給付額を増やすことで、従業員の引き留めが図れます。定年時に十分な年金を付与することで、高齢者の引退を促進することができます。結果として、従業員の新陳代謝が図れます。
企業年金の制度コンサルとは、このような企業の人事戦略のニーズにこたえるコンサルティングを行うことです。これは人事部から見た側面ですが、変更した制度が企業会計にどのような影響を与えるのかという財務的な視点も欠かせません。複数の利害関係者の意見を調整しながら、法令や数理的な知識をいかし、企業にとってのベストな選択肢を提供するのが年金コンサルの醍醐味です。
(狭義の)年金数理が対象とする領域は、「保険料の計算」と「決算」です。保険料の計算が必要となる場面は多岐にわたります。
- 企業年金を発足した場合
- 企業年金の制度設計を見直した場合
- 予定利率を見直した場合
- 財政再計算
- 企業年金の分割や合併 など
これらの場面に共通するのが、現在価値が変わる、という点です。制度設計を変更すると、給付額が変わります。予定利率を見直すと、割引率が変わります。財政再計算を行うと、計算基礎率を見直すことになるので、給付額は変わらなくてもその期待値は変わります。
$$ 現在価値 = \frac{A(1)}{1+i} + \frac{A(2)}{(1+i)^2} + \frac{A(3)}{(1+i)^3} + ... $$
その結果、保険料をどのように見直すべきか。これが年金数理における主な考察対象です。
また、企業年金も通常の企業と同様、年に一回決算を行っています。決算では、一年間の収支を把握するとともに、当年度に発生した剰余や不足を把握することが主な目的です。企業年金のバランスシートを見ると、その大部分を占めるのが「責任準備金」です。これは、生命保険会社と共通しています。この責任準備金を計算するのが、年金アクチュアリーの主要な仕事です。
また、受託機関によっては、企業年金に一人の年金数理人をアサインすることで、継続的な視点で企業年金の財政状況に関するアドバイスを行う会社もあります。アサインされた年金数理人にとって、年に一度の決算報告も重要な仕事です。単に、P/LやB/Sの報告にとどまらず、なぜ剰余になったのか、不足になったのかの説明も行います。この仕組みをカバーしているのが、実務編の第3章の内容です。
●「年金数理とは」のまとめ
- 狭義の年金数理の主な考察対象は、退職金とDB。
- 退職金と企業年金は切っても切れない関係にある。
- DBの給付設計には、定額、最終給与比例、累積給与比例、ポイント制、CB制度の5種類がある。
- DBの給付は一時金ベースで決まる。年金額は一時金原資と等価になるように設定される(但し、保証期間付き終身年金は要注意)
- 利率には、予定利率、据置利率、給付利率がある。CB制度の場合は、予定利率、加入中の利率、据置中の利率、受給中の利率があり、予定利率以外は一般に変動する。
年金数理の基本原理
教科書では、「大数の法則」「収支相等の原則」「非負の原則」が挙げられています。この部分は、試験で問われることはありませんが、何れも基本的な概念なので、サラッと理解しておきましょう。
大数の法則
「百聞は一見にしかず」ということで、「一時金選択率」を使ってシミュレーションしてみます。一時金選択率とは、年金受給資格を満たして退職した人のうち、何割が一時金を選択するかという計算基礎率の一つ。ここでは、平成30年就労条件総合調査をもとに7割でセットしています。
以下のグラフを見ると、人数が少ない場合、ばらつきが大きくなっていることがわかります。
企業年金の加入者数が少ないと、計算基礎率のばらつきが大きくなり、毎年の決算で剰余・不足が生じやすくなります。また、財政再計算で計算基礎率を見直す場合、保険料の水準が大きく変わる可能性があります。このようなリスクのことを、CERAではレベルリスクと呼んでいます。
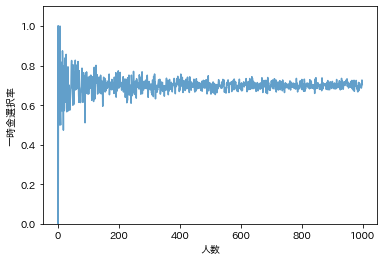
import matplotlib.pyplot as plt
import random
import japanize_matplotlib
n=1
prob=[]
num=[]
random.seed(1)
while n < 1000:
lumpsum = 0
annuity = 0
for i in range(n):
if random.uniform(0,1) < 0.7:
lumpsum +=1
else:
annuity +=1
k = lumpsum / (lumpsum + annuity)
prob.append(k)
num.append(n)
n +=1
plt.plot(num, prob, alpha=0.7)
plt.xlabel('人数')
plt.ylabel('一時金選択率')
plt.ylim(0,1.1)
plt.show()
収支相等の原則
掛金の総額+積立金の運用収益の総額=給付の総額
これが収支相等の原則の考え方です。
生保数理の場合、保障期間という概念があって、その期間において個人の収支が相等するように保険料を決めます。
教科書では、企業年金制度と厚生年金保険で、対象と期間を区別して書いていますが、正直この説明だけ読んで理解できる人はいないと思います。ここで伝えたいことは、既述の「企業年金は集団単位で収支相等」という点と、その集団には「将来加入者」を含むケースと含まないケースがある、という点です。将来加入者とは、将来企業年金に加入する人のことです。この集団を想定すると、期間は無限期間と考えられるので、教科書のような記載となっています。第3章の財政方式を勉強すると、この違いがわかると思います。
非負の原則
これは、他の年金数理の文献を見ても登場しない、教科書特有の記載です。積立金が不足して給付できない、という事態は避けなければならないというのが非負の原則の考え方。CERAでいうところの、流動性リスク管理です。
事前積立方式の場合、起こりにくいイベントですが、公的年金のような賦課方式で財政運営を行っている場合に留意すべきポイントです。日本の公的年金も賦課方式で運営されていますが、積立金を有しています。5年に一度の財政検証では、約100年間の収支のシミュレーションを行い、その時点の積立金が支出の1年分となるような財政見通しを作成しています。ここで「支出の1年分」を用いているのは、非負の原則の考え方に基づくものです。
●「年金数理の基本原則」のまとめ
- 給付を賄うための原資は掛金と運用利息。
- 収支相等の原則を考える場合、将来加入者を加味する場合と加味しない場合がある。
計算基礎率
抑えておくべき計算基礎率は以下のとおりです。
- 予定利率
- 予定死亡率
- 予定脱退率
- 予定昇給率
- 新規加入の見込み
- 一時金選択率
- CB制度で用いる利率の見通し
このように、年金数理では生保数理よりも多くの計算基礎率を必要とします。なぜか?
その理由も、何度か登場している現在価値の数式を思い出すとわかると思います。予定利率を割引計算に用いるのは生保数理と同様です。一方、給付額の期待値\(A(t)(t=1,2,3,...)\)は、予定死亡率だけでなく予定脱退率にも依存します。給与を用いた給付設計の場合、将来の給与も予測する必要があります。財政方式によっては、新規加入の見込みも必要です。退職者が年金を選択するのか、一時金を選択するかによって、企業年金のキャッシュフローは変わります。CB制度の場合、利率が変動するので、一定の前提が必要です。このような理由から、年金数理では多くの計算基礎率を仮定する必要があります。
$$ 現在価値 = \frac{A(1)}{1+i} + \frac{A(2)}{(1+i)^2} + \frac{A(3)}{(1+i)^3} + ... $$
これらの計算基礎率は、すべての給付設計で用いられるものでしょうか?
答えはNOです。
以下の表で、給付設計と計算基礎率の対応をまとめてみました。実務で最も用いられている加入年齢方式を想定して〇×をつけたものです。
| 定額 | 最終給与 | 累積給与 | ポイント制 | CB制度 | |
| 予定利率 | 〇 | 〇 | 〇 | 〇 | 〇 |
| 予定死亡率 | 〇 | 〇 | 〇 | 〇 | 〇 |
| 予定脱退率 | 〇 | 〇 | 〇 | 〇 | 〇 |
| 予定昇給率 | × | 〇 | 〇 | 〇 | 〇(定額CBは×) |
| 新規加入の見込み | 〇 | 〇 | 〇 | 〇 | 〇 |
| 一時金選択率 | 〇 | 〇 | 〇 | 〇 | 〇 |
| CB利率の見込み | × | × | × | × | 〇 |
計算基礎率のうち、試験に出題されやすい「予定昇給率」と「CB制度で用いる利率の見通し」について補足します。
予定昇給率
予定昇給率を用いた典型的な問題は、以下のようなものです。

この問題を解くのに必要な知識は以下の3つです。
- 静態的昇給率(Rx):ベースアップを見込まない昇給率
- 動態的昇給率(R'x):ベースアップを見込んだ昇給率
- ベースアップ(r):物価上昇等にあわせて賃金水準全体を引き上げること
この3つには、以下のような関係があります。
$$ 1+R'_x = (1+R_x)(1+r) $$
第1章の練習問題7や8にも昇給率に関する問題があるので、各自で解いてみましょう。
CB制度で用いる利率の見通し
CB制度の例示を再掲すると、

仮想個人勘定残高をもとに一時金額や年金額の計算を行うのがCB制度でした。ここで登場するのが、加入中の利息、据置中の利息、受給中の利息です。繰り返しになりますが、これらは予定利率とは別物です。
CB制度の一番の特徴は、加入中・据置中・受給中の利息を計算する利率が、国債の利回り等を用いて変動するという点です。将来の国債の利回りを現時点では把握することはできません。「将来の支払額を予測」するためには、一定の前提をおいて計算を行う必要があります。この前提がCB制度で用いる基礎率です。
「年金数理」の試験対策という意味では、加入中・据置中・受給中の利率が変わり得る、という点だけ抑えておけば十分ですが、以下のCB制度の意義についても知っておくとよいと思います。
キャッシュバランス制度は、利息クレジット率を市場金利に連動させるケースが多い。そのため、例えば金利が低下すると、債務評価上の割引率が低下して給付現価が増加する一方で、将来の利息クレジットが低下することで給付の見込み額が減少するため、互いの変動要素が相殺され、制度運営が金利変動の影響を受けにくいとされる。
アクチュアリー数学シリーズ③「年金数理」の25~26頁
この記載も、現在価値の数式を用いて解釈すると、
- 「金利が低下すると、債務評価上の割引率が低下して給付現価が増加」⇒ \( i \) が低下すると、\( \frac{1}{1+i} \) が増加
- 「将来の利息クレジットが低下することで給付の見込み額が減少」⇒ \( A(t) \)が減少
ということになります。
$$ 現在価値 = \frac{A(1)}{1+i} + \frac{A(2)}{(1+i)^2} + \frac{A(3)}{(1+i)^3} + ... $$
●「計算基礎率」のまとめ
- 年金数理で扱う計算基礎率は生保数理よりも多い。
- 昇給率には、静態的昇給率と動態的昇給率の2つの考え方がある。
- CB制度の場合、加入中/据置中/受給中の利率が変動する可能性があるので、計算基礎率として「利率の見通し」を用いる必要がある。
定常人口
シンプルなケースを考えます。
- DBの新規加入年齢は30歳
- 毎年100人がDBに加入
- 加入のタイミングは期初
- DBから脱退する確率(死亡も含む)は、30歳が1/4、31歳が3/1、32歳が1/2、33歳が1
この場合、企業年金の人数をシミュレーションしてみましょう。
| 年度 | 30歳 | 31歳 | 32歳 | 33歳 | 34歳 | 合計人数 | |
| 1 | 新規加入者⇒ | 100 | 100 | ||||
| 2 | 新規加入者⇒ | 100 | 75 | 175 | |||
| 3 | 新規加入者⇒ | 100 | 75 | 50 | 225 | ||
| 4 | 新規加入者⇒ | 100 | 75 | 50 | 25 | 250 | |
| 5 | 新規加入者⇒ | 100 | 75 | 50 | 25 | 0 | 250 |
| 6 | 新規加入者⇒ | 100 | 75 | 50 | 25 | 0 | 250 |
| 定常人口の分布 | 40% | 30% | 20% | 10% |
これが、教科書の以下の記載が意味することです。
毎年、一定人数が一様に出生し、死亡率のとおりに死亡し、かつ人口の移出入のない社会を仮定すると、その社会の年齢構成はやがて一定の状態に達する。これを死亡率の示す定常人口という。同様にして、企業の従業員集団においても、毎年特定の年齢で一定人数が入社し、予定されている脱退率に従い脱退・死亡するものと仮定した場合、やはり定常人口に達することになる。これを脱退残存表の示す定常人口という。
教科書の13頁
人口統計学の世界では、ロトカの命題として知られているものです。
封鎖人口において、ある時点以降の年齢別死亡率と年齢別出生率が不変であるという仮定をおけば、人口増加率はある一定値に収束するとともに、その人口の年齢別人口割合も収束する。またこのように収束した年齢構造は、当初の年齢構造とは独立に、もっぱら年齢別死亡率と年齢別出生率によって定まる。
「人口統計学の理論と推計への応用」の91頁
教科書13頁の記載は、ロトカの命題の条件を満たすので、年齢構成が一定の状態に収束することとなります。この収束した状態を安定人口(stable population)と呼びます。
なお、ロトカの命題は、年齢構成の収束を意味するもので、出生率と死亡率に差があると、人口規模の増減はあり得ます。安定人口であって、人口の増減がない場合を、一般に定常人口(stationary population)と呼んでいます。
上記の例を見ると、安定人口に達した後、合計人数の変動はありません。これは、新規加入者が100人で、脱退者も100人(各年齢で25人ずつ)と、新規加入者と脱退者に差がありません。したがって、これは定常人口の例ということになります。
生命表
ここも、百聞は一見にしかず、ということで生命表を見てみましょう。

以上を踏まえて、少しだけひねった問題を解いてみましょう。
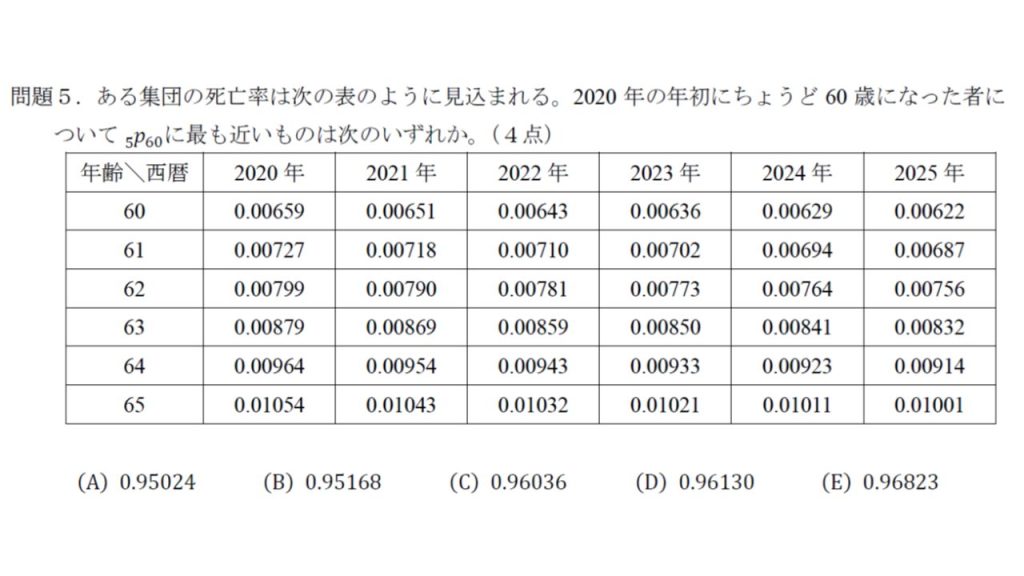
これも、実務家は背景が推察できる問題ですが、学生からすると教科書には載っていないと感じるタイプの問題です。年金数理人会は2012年に「IAS19における死亡率の取扱い報告」を公表しています。IAS19とは、退職給付会計に関する国際基準のことで、このあたりから年金アクチュアリーは、将来の死亡率改善を加味した実務を検討するようになりました。この問題でも、各年齢の死亡率が少しずつ改善してますよね。
次は、よく出題される「平均余命」です。「平均」余命という名のとおり、これは何かの平均を表しています。
略算平均余命は以下のように計算されます。

ここで、最初の等式を見ると、第1項が0×死亡確率、第2項が1×死亡確率、第3項が2×死亡確率となっています。この死亡確率をすべて足すと1になります。なぜなら、各項の確率はx歳の人が1年以内に死亡する確率、1年~2年以内に死亡する確率・・・を表しており、人はいつか死亡するので、その合計は1となります。一方、死亡確率にかかる数値は、0、1、2と一ずつ増えています。この数値は期間を意味するもので、1年以内に死亡する場合は0(即ち、端数月を切り捨て)、1年~2年以内に死亡する場合は1(ここでも、端数月を切り捨て)・・・を表しています。「略算」というのは、端数月を切り捨てる、ということを意味するものです。
最後に、死力を見てみましょう。死力を考える場合、\(l_x\)は年齢が整数値のときに定義される関数ではなく、連続的な曲線で表現されるものとして考えます。死力は確率ではありません。したがって、死力は1を超える可能性があります。(詳しく知りたい人は、「生命保険数学の基礎」を参照)

以下の法則を覚えておくと、計算時間の短縮につながります。
| \(\mu_x \) | \(\, _t p_x \) | 完全平均余命 | |
| 死力一定 | \(\mu\) | \( e^{-\mu t} \) | \( \frac{1}{\mu} \) |
| ド・モアブルの法則 | \( \frac{1}{\omega - x} \) | 1 - \( \frac{t}{\omega - x} \) | \( \frac{\omega - x}{2} \) |
死力一定の場合、
\(\, _t p_x = e^{-\int_0^t \mu_{x+s} ds} = e^{-\int_0^t \mu ds} = e^{-\mu t} \)
完全平均余命= \( \int_0^{\omega - x} \, _t p_x dt = \int_0^{\omega - x} e^{-\mu t} dt = \frac{1}{\mu} \)
ド・モアブルの法則とは、\( l_x = l_0 \frac{\omega -x}{\omega} \) のように、生存数が等差数列的に減少するという法則のこと。
\(\mu_x = - \frac{dl_x}{l_x dx} = - \frac{\omega}{l_0(\omega - x)} \frac{-l_0}{\omega} = \frac{1}{\omega - x}\)
\(\, _t p_x = \frac{l_{x+t}}{l_x} = \frac{\omega -x-t}{\omega -x} =1 - \frac{t}{\omega - x} \)
完全平均余命= \( \int_0^{\omega - x} \, _t p_x dt = \int_0^{\omega - x} \, (1 - \frac{t}{\omega - x} ) dt = \frac{\omega - x}{2} \)


\( e_x = p_x + \, _2p_x + \, _3p_x + ... = p_x + p_x(p_{x+1} + \, _2p_{x+1} + ...) =p_x (1+ e_{x+1}) \)
1つ目の重要公式の証明は簡単ですね。
2つ目の重要公式も定義に分数の微分を適用すると、
\( \frac{d \, _tp_x}{dx} = \frac{d}{dx} \frac{l_{x+t}}{l_x} = \frac{\frac{dl_{x+t}}{dx} \,l_x - l_{x+t} \, \frac{dlx}{dx}}{l_x^2} = \frac{-l_{x+t} \,\mu_{x+t} \, l_x + l_{x+t} \, l_x \, \mu_x}{l_x^2} = \, _tp_x (\mu_x - \mu_{x+t})\)
3つ目の重要公式は、平均余命の定義式に2つ目の公式を代入すると導出できます。(ただし、微分と積分の交換は可能という仮定が必要)
以上の知識があれば、以下の問題を解くことができます。

思考のステップは以下のとおりです。
- 完全平均余命の式が与えられている
- \( l_{0} \)が所与で、\( l_{40} \)を求めるということは、\(\, _{40} p_0 \)を求めればよい
- 完全平均余命と\(\, _t p_x \)は定義式の関係があるけど・・・、右辺に積分があるので、両辺を微分したくなる
- ということは、完全平均余命の微分公式が使えるかも ⇒ 死力がわかる
- 死力がわかれば、死力と\(\, _t p_x \)の関係式は知っているので、\(\, _t p_x \)が求まる
- 死力を計算すると、ド・モアブルの法則に従うことに気づく(完全平均余命の数式を見て、ド・モアブルの法則であることに気づくのが最短ですが、ここまでのステップは他の問題でも応用可能な思考プロセスなので、あえてここで気づくことにしています)
- \(\, _{40} p_0 = 1-\frac{40}{100} = 3/5 \)なので、\( l_{40} \)は60,000
教科書の第1章練習問題の2にも類似の問題があるので要チェックです。
生命表に関する記号は生保数理と共通です。以下の動画を見ると、復習になると思います。
脱退残存表
生保数理でいうところの、多重脱退表に相当する概念です。企業年金の場合、死亡脱退、自己都合脱退、会社都合脱退で給付が異なることがあります。これは、退職事由別の乗率を設けている退職金制度が多いことに由来するもので、それを移行したDBも同様に給付に格差がついています。一般に、自己都合脱退の方が、他に比べると退職事由別の乗率が小さく、どの程度の減額率が用いられるかは、個々の企業の人事施策によります。
以下の表は、教科書の17頁からの脱退残存表の一部を抜粋したものです。観測される生存脱退数は死亡脱退による影響を受けた後の脱退数であり、死亡脱退数も生存脱退の影響を受けています。生存脱退したあとの死亡を把握するすべがないからです。観測される死亡脱退数を用いて死亡率を計算すると、本来の死亡率を過小評価することになります。この本来の死亡率のことを絶対死亡率と呼びます。

「エクスポージャ」という年金数理には登場しない概念ですが、これを使うと教科書の(1-15)式の意味合いが理解しやすいと思います。((1-15)式は下図の矢印が指す数式のこと)
「エクスポージャ」は損保数理に登場する概念ですが、これは損保特有の概念ではなく、アクチュアリアル・サイエンス全般に共通する考え方です。「expose」の意味をdictionary.comで調べると「to lay open to danger, attack, harm, etc.」となっています。リスクにさらされている、というようなニュアンスです。死亡率を計算する際の分母に相当する概念です。
脱退残存表に話を戻します。「死亡脱退」というリスクを考えます。この死亡脱退というリスクにさらされている人(すなわち、エクスポージャ)は、どのように考えればよいでしょうか?
まず、生存脱退が「期初」に起こるケースを考えます。期初に脱退した人は、(企業年金からの)死亡脱退というリスクにさらされていないので、残存数から生存脱退者数を控除した人数がエクスポージャとなります。
一方、生存脱退が「期末」に起こる場合、当該脱退者は、(企業年金からの)死亡脱退というリスクにさらされているので、残存数から控除する必要はありません。
教科書の18頁にあるように、年金数理では「生存脱退が1年を通じて一様に分布する」と仮定します。一様に分布するということは、平均的には期央で発生するということです。期央で発生するので、期中の生存脱退者については半分だけ除外すればよい(すなわち、エクスポージャは期初と期末の和半)ことがわかります。
これが、(1-15)式が意味することです。
脱退残存表に関する典型的な問題は、以下のような穴埋め問題です。
スクロールを止めて、実際にこの問題を解いてみましょう。
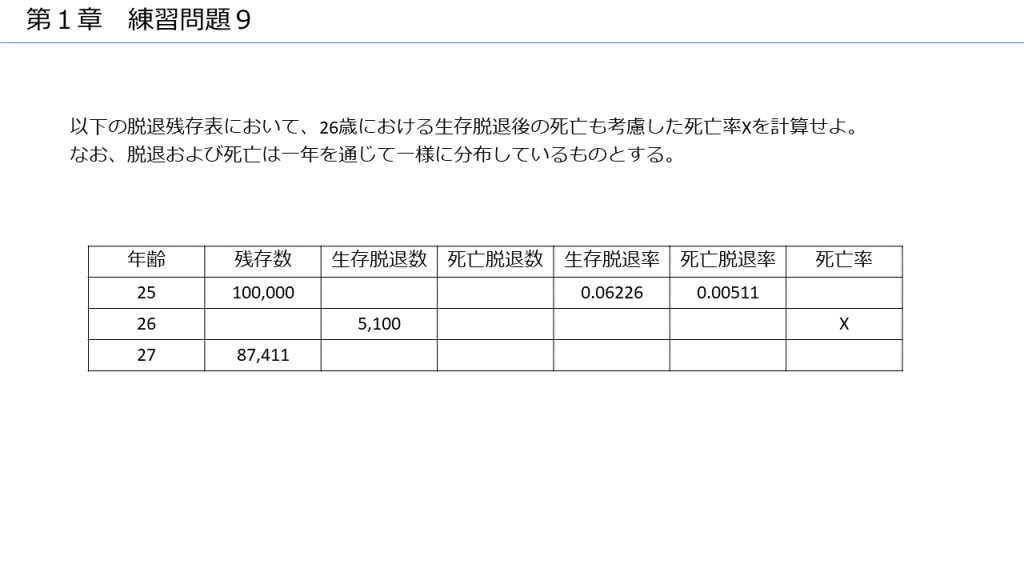
解答は以下のとおり。赤字部分は、所与の数字から順番に計算できると思います。26歳の死亡率を計算するには、(1-15)式を覚えておく必要があります。覚え方は、「期央なので、エクスポージャの生存脱退者は半分だけ引く」というものでしたね。

以下は、もう少し厳密な議論を好む方向けの説明です。
脱退残存表の説明の途中で、「一様に分布する」という仮定が登場しました。これは、英語ではUDD(Uniform Distribution of Death)の仮定として知られているものです。
まずは、通常の生命表で考えます。
$$ _r \, q_x = Pr(T_x \leq r) = Pr(U<r \cap K_x = 0) = Pr(U<r) Pr(K_x = 0) =r q_x$$
ここで、
- \(T_x \)は\(x\)歳の人の余命を表す確率変数
- \(K_x \)は\(x\)歳の人の略算余命を表す確率変数
- \(U\)は[0,1]区間の一様分布を表す確率変数、\(U\)と\(K_x \)は独立
- \(r\)は0以上1未満の数値
したがって、例えば\(r=0.5\)の場合、\( _{0.5} \, q_x = 0.5 q_x\)となります。
この考え方を、脱退残存表に拡張します。この場合、「一様に分布する」という仮定は、SUDD(Singleな生命表がUDDという意味)と呼ばれ、絶対脱退率(右肩に*をつけて区別)の生命表がUDDであることを想定します。そうすると、
$$ _r q_x^{(d)*} = r q_x^{(d)*}$$
$$ _r q_x^{(w)*} = r q_x^{(w)*}$$
絶対脱退率についても、「死力(or 脱退力)」という概念を定義することができます。この脱退力を用いると、絶対脱退率は、
$$ q_x^{(d)*} = \int_0^1 \, _s p_x ^{(d)*} \mu_{x+s}^{(d)} ds $$
$$ q_x^{(w)*} = \int_0^1 \, _s p_x ^{(w)*} \mu_{x+s}^{(w)} ds $$
そして、観測される脱退率は、脱退残存表で観測される生存率\(\, _s p_x ^{(T)}\)を用いて、以下のようにあらわすことができます。
$$ q_x^{(d)} = \int_0^1 \, _s p_x ^{(T)} \mu_{x+s}^{(d)} ds $$
$$ q_x^{(w)} = \int_0^1 \, _s p_x ^{(T)} \mu_{x+s}^{(w)} ds $$
ここで、死力の定義を思い出すと、
$$ \mu_{x+t} = -\frac{1}{l_{x+t}} \frac{dl_{x+t}}{dt} = -\frac{1}{_t \,p_x} \frac{d \,_t \, p_x}{dt}$$
なので、
$$ _t \,p_x \mu_{x+t} = - \frac{d \,_t \, p_x}{dt} $$
UDDの仮定を使うと、
$$ _t \,p_x \mu_{x+t} = - \frac{d}{dt}(1-\,_t \, q_x) = - \frac{d}{dt}(1- t \, q_x) = q_x$$
となります。これは、絶対脱退率についても成立します。
死亡脱退と生存脱退の独立性を仮定すると、
$$ q_x^{(d)} = \int_0^1 \, _s p_x ^{(T)} \mu_{x+s}^{(d)} ds = \int_0^1 \, _s \, p_x^{(w)*} \, _s \, p_x^{(d)*} \mu_{x+s}^{(d)} ds = \int_0^1 \, _s \, p_x^{(w)*} q_x^{(d)*} ds $$
$$ = \int_0^1 \, (1 - \,_s \, q_x^{(w)*}) q_x^{(d)*} ds = \int_0^1 \, (1 - s \, q_x^{(w)*}) q_x^{(d)*} ds $$
$$ = q_x^{(d)*} \lbrack s - \frac{1}{2} s^2 \, q_x^{(w)*} \rbrack _0^1 = q_x^{(d)*} \lbrack 1 - \frac{1}{2} \, q_x^{(w)*} \rbrack$$
これは、生保数理のテキスト上巻の(3.2.6)式に対応します。
右辺のかっこを左辺に移行すると、
$$ q_x^{(d)*} = \frac{q_x^{(d)}}{\lbrack 1 - \frac{1}{2} \, q_x^{(w)*} \rbrack} $$
となり、年金数理のテキストの(1-15)式に近い関係式となりました。でも、右辺の分母に*があるので、(1-15)式とは微妙に違います。実は、(1-15)式は実務で用いられている近似式であり、伝統的には(1-15)式が用いられています。
これは当初求めた(略)とは明らかに異なっており、正確ではない。この概算値は、あからさまに言えば、分母に残っている\(q_x^{A*}\)や\(q_x^{B*}\)の”*”を消しゴムでこっそり消したようなことになっており、一見勧められるものではないが、これはある限定的な範囲内ではきわめて有効なのである(さらに伝統的にこの方式が用いられてきた)。
「生命保険数学の基礎」の323頁
絶対脱退率については、年金数理のテキストには言及がありませんが、過去問では出題されています。生保数理のテキスト第3章「脱退残存表」もセットで読むことをお勧めします。
計算基数
パソコンや電卓が普及し、高速で計算を繰り返すことができるようになる以前は、アクチュアリーたちは、計算基数と呼ばれる関数群を用いて、簡単に保険数理上の現在価値を算出していました。これらの関数は、生存率の決定論的モデルと、一定かつ平準化された利回りに基づいています。このモデルがあれば、様々な保険数理計算のための情報を効率的に要約することができます。
技術の進歩に伴い、計算基数の限界も明らかになってきました。この関数は、選択期間中の脱退、金利の変動、不規則な給付の増額には適していません。これらの関数は、基本的な原理とコンピュータやプログラム可能な計算機による高速計算を利用して組み込むことができます。さらに、技術の進歩により、アクチュアリーは決定論的モデルから確率論的モデルへと拡張し、変化幅をもつリスクについての課題に対応できるようになってきました。
私たちは今、転換期を迎えています。計算を簡略化するために計算基数はもはや必要ではなくなりましたが、計算基数は今でも様々な保険数理計算の記述方法として一般的であり、多くのコンピュータプログラム、書籍、政府の規制の中で見られます。
米国アクチュアリー会のスタディ・ノート「Comutation Functions」(1999)の仮訳
1999年の米国アクチュアリー会の文献に、このような記述があります。一方、日本のアクチュアリー実務では、依然として計算基数が使われています。これは、生保や年金が長期契約に基づくもので、過去から連綿として使われている計算基数をなくすことはできないという制約によるものです。過去の年金制度や保険商品の数理的な仕組みを見るには、計算基数が読めなくてはなりません。

金利計算
企業年金は、一部の財政方式を除き、積立金が形成されます。収支相等の原則にあるように、積立金の運用収益を見込んで掛金の計算を行います。
掛金の総額+積立金の運用収益の総額=給付の総額
年金数理では、複利を前提に数理計算を行います。

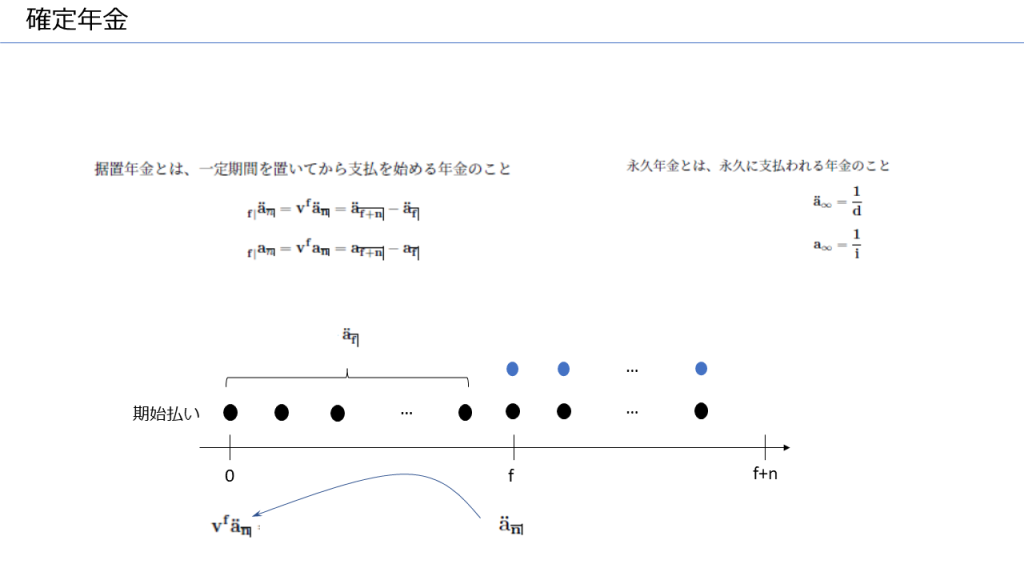
確定年金
日本の多くのDBは確定年金を採用しています。これも、日本の企業年金は退職金を移行する形で設計されていることが理由です。
DBの給付設計の部分で説明したように、退職金移行のDBは、以下の2ステップで設計します。
- 一時金額の額計算する
- 一時金額をベースに年金額の計算を行う
この2つ目の年金額の計算で用いられるのが確定年金現価率です。具体的には、
一時金額=年金額×確定期間の確定年金現価率
となるように、年金額を計算します。ここで用いる確定年金現価率は、年金の支払い方に応じて決定されます。

ここまで年一回払いを想定していましたが、実際の年金は年6回払いのような形で支給されます。したがって、年金現価率も年k回払いという概念が必要となってきます。


ここまで理解した方は、以下の2問を解いてみましょう。
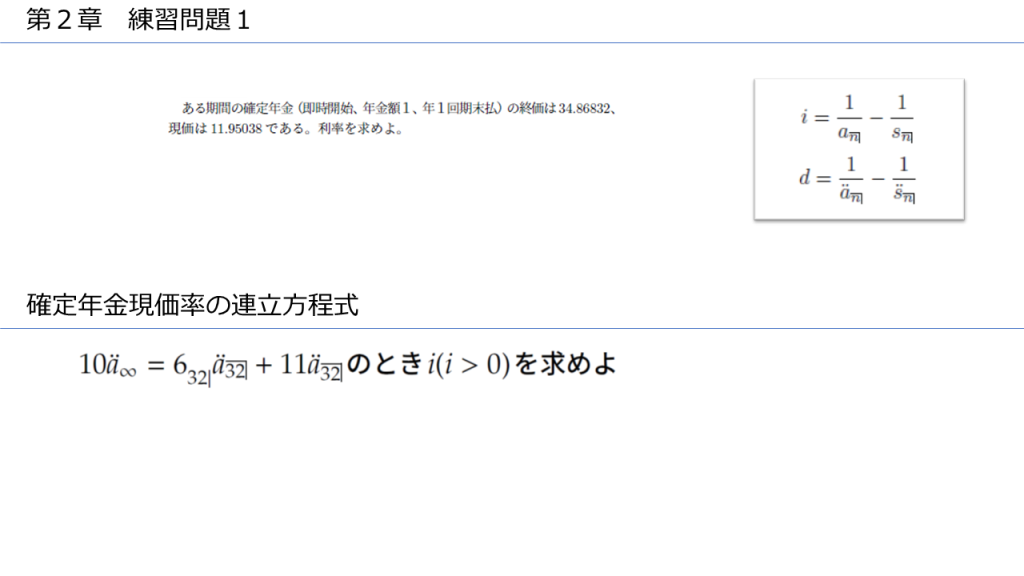
\( x = v^{32} \)とすると、この連立方程式は、
$$ 10 \frac{1}{d} = 6x \frac{1-x}{d} + 11\frac{1-x}{d} $$
$$ 10 = 6x(1-x) + 11(1-x) $$
$$ 6x^2 + 5x -1 =0 $$
$$ (6x-1)(x+1) =0 $$
\(x >0\) なので、\(x=\frac{1}{6} \)となり、あとは電卓を叩けば \(i \)を求めることができます。
生命年金
日本のDB制度で終身年金を採用している制度は多くありません。これも、退職金という、企業にとって長寿リスクのない制度がベースになっていることに起因します。
なぜ企業は年金制度を実施するのか。その理由の一つに「Paternalism」が挙げられることがあります。この考え方にもとづくと、退職金移行のDBが終身年金を提供することも考えられますが、実態はそうではなく、終身年金の実施割合は減少しています(企業年金・個人年金部会の第1回資料参照)。
終身年金のキャッシュフローは永久年金と似ていますが、支払時期までの生存確率を加味する点が異なります。

有期生命年金のキャッシュフローは確定年金と似ていますが、支払時期までの生存確率を考慮する点が異なります。

確定年金と同様、生命年金についても据置タイプの年金を考えることができます。

保証期間付き終身年金は、厚生年金基金(2014年以降の新規設立は不可)で採用されていたことから、昔は見かける機会が多いタイプの年金でした。その名残もあって、試験でも時々取り上げられることがあります。
保証期間付き終身年金の現価は、以下のように、確定年金と据置年金の和であらわすことができます。

以下の公式は、試験で直接問われる機会はあまりありませんが、回答を導く過程で用いることが多いという意味で重要な公式です。期初払いと期末払い、年齢や支払期間が1ずれているケースなど、キャッシュフローをイメージすると、理解の手助けになると思います。


確定年金と同様、年k回払いや連続払いの生命年金を考えることもできます。


ここまで理解した方は、以下の問題を解いてみましょう。

変動年金
ここまで、年金のキャッシュフローは年金額1で考えていましたが、年金額が変動するタイプの年金のキャッシュフローを考えることもできます。


年金額が徐々に減っていくタイプの変動年金です。その現価をAとすると、
$$ A = 2n + (2n-1) vp_x + (2n-2) v^2 \, _2 p_x + ... + (n+1) v^{n-1} \, _{n-1} p_x $$
ここで、最後の項だけ変形すると、
$$ A = 2n + (2n-1) vp_x + (2n-2) v^2 \, _2 p_x + ... + (2n - (n-1)) v^{n-1} \, _{n-1} p_x $$
となるので、
$$ A = 2n(1+vp_x + v^2 \, _2 p_x + ... + v^{n-1} \, _{n-1} p_x) - (vp_x + 2 v^2 \, _2 p_x + ... + (n-1) v^{n-1} \, _{n-1} p_x)$$
右辺の第1項のかっこ内は、期初払い有期年金の年金現価率ですね。その公式を思い出すと、
$$ 第1項のかっこ内=\frac{N_x - N_{x+n}}{D_x} $$
右辺の第2項は、
$$ 第2項= \frac{D_{x+1} + 2D_{x+2} + ... + (n-1) D_{x+n-1}}{D_x} $$
$$ = \frac{(D_{x+1} + D_{x+2} + ... + D_{x+n-1}) + (D_{x+2} + D_{x+3} + ... + D_{x+n-1}) + ... + D_{x+n-1}}{D_x} $$
$$ = \frac{(N_{x+1} - N_{x+n}) + (N_{x+2} - N_{x+n}) + ... + (N_{x+n-1} - N_{x+n})}{D_x}$$
$$ = \frac{S_{x+1} - S_{x+n} - (n-1)N_{x+n}}{D_x}$$
したがって、
$$A = \frac{2n(N_x - N_{x+n}) - (S_{x+1} - S_{x+n} - (n-1)N_{x+n})}{D_x} $$
$$= \frac{2nN_x - nN_{x+n} - (S_{x+1} - S_{x+n} + N_{x+n})}{D_x} $$
$$= \frac{2nN_x - nN_{x+n} - (S_{x+1} - S_{x+n+1})}{D_x} $$
連生年金
生命確率、死力、平均余命の概念を単一の人ではなく、複数人に拡張することができます。




複数人に拡張した生命確率などを用いることで、複数人の生死に関連するキャッシュフローの評価を行うことが可能となります。


年金の支払い条件を表で整理すると、
| x | y | z | 合計年金額 | |
| ① | 〇 | 〇 | 〇 | 6 |
| ② | 〇 | 〇 | × | 5 |
| ③ | 〇 | × | 〇 | 5 |
| ④ | 〇 | × | × | 0 |
| ⑤ | × | 〇 | 〇 | 6 |
| ⑥ | × | 〇 | × | 4 |
| ⑦ | × | × | 〇 | 4 |
| ⑧ | × | × | × | 0 |
求める年金の現価をAとすると、
$$ A = \alpha_1 a_x + \alpha_2 a_y + \alpha_3 a_z + \beta_1 a_{xy}+ \beta_2 a_{yz}+ \beta_3 a_{zx} + \gamma a_{xyz}$$
ここで、一人だけ生存しているケース(④、⑥、⑦)を考えます。この場合、Aの右辺で考えるべきは最初の3つの項のみです。その他の現価はゼロなので。
合計年金額が年金現価の係数になるので、
$$\alpha_1 =0$$
$$\alpha_2 =4$$
$$\alpha_3 =4$$
次に、二人だけ生存しているケース(②、③、⑤)を考えます。ここでも、右辺で残る項を考えると、
$$ 4 + \beta_1 =5 \, \rightarrow \beta_1 =1$$
$$ 4 + \beta_3 =5 \, \rightarrow \beta_3 =1 $$
$$ 8 + \beta_2 =6 \, \rightarrow \beta_2 =-2$$
最後に、三人全員が生存しているケース①を考えます。
$$ 8+1-2+1+\gamma = 6 \, \rightarrow \gamma=-2 $$
教科書の第1章と第2章の復習


