イールドカーブと生保数理
生命保険アクチュアリーは、しばしば予定利率として固定した1つの利率を使用してきた。この理由は、計算の簡便性のみならず、契約の超長期性を考慮すると、契約期間に合わせた長期金利よりも、保守的な低い利率を設定しておけば保険料や責任準備金の十分性は担保される、という暗黙の理解があったためであろう。また、保守的な評価を行っていても、有配当保険契約であれば契約者配当という事後的な精算の手段があり、契約者間の公平性は保持できると考えられていた。しかし、株主からは保険料の低廉化や生保会計に対する透明性の高い評価が要請されるようになり、金融市場と整合的な資産・負債の評価が求められるようになってきた。
Rによるアクチュアリーの統計分析(田中周二)
実務上、金利は投資期間に応じて変化する。
つまり、例えば5年間投資した金額は、15年間投資した金額や6ヶ月間投資した金額とは異なる金利を得ることになる。
\( v(t) \) を、t年のゼロクーポン債の現在の市場価格、つまり、t年後に確実に単位金額を支払う投資の現在の市場価格を表すものとする。
なお、\(v(t)\)の値は、市場での取引の結果、いつでも変化する可能性があるものの、少なくとも原理的には不確実性はない。
t年目のスポットレート(\(y_t\)と表記)は、このゼロクーポン債の1年ごとの利回りである。
$$ v(t) = (1+y_t)^{-t} $$
金利の期間構造とは、投資の期間と投資にかかる金利の関係を表したもので、イールドカーブとして図示される。
伝統的な生保数理では、フラットな期間構造を想定していた。
この仮定により、任意の期間tに対する割引関数として\(v^t\)を使用することができ、vは定数となる。
この仮定を緩めて、金利が期間によって変化するようにすると、\(v^t\)の割引関数はもはや適切ではない。
期間構造がある場合は、将来の各支払額を、その支払期日までの期間に応じたスポットレートの金利を使って割り引くことになる。
あらゆるキャッシュフローの現在価値は、そのキャッシュフローを正確に複製するポートフォリオを購入するためのコストとなる。
今、t年のゼロクーポン債に金額\(v(t)\)を投資すると、t年後には1になるので、\(v(t)\)は\(v^t\)を一般化した割引関数と解釈できる。
実務で登場するイールドカーブ
年金アクチュアリーは、退職給付債務の計算業務において、イールドカーブを用いる。
イールドカーブは、期間の異なるスポットレートの集合である。スポットレートは、割引債(期中での利息の支払いがなく満期での支払いのみを約束する債券)の利回りである。イールドカーブは、①市場データをもとにユニバースを設定し、②ユニバースに含まれるデータに対してモデルを用いて推定することによって得られる。
退職給付会計に関する数理実務ガイダンス
数理実務ガイダンスには、パラメトリックなモデルとスプラインベースのモデルが例示されている。
パラメトリックなモデル
- ネルソン・シーゲル・モデル
- スヴェンソン・モデル
スプラインベースのモデル
- 多項スプライン(例、McCulloch)
- 指数スプライン(例、Vasicek and Fong)
- B スプライン(例、Steeley)
生保・損保アクチュアリーの場合、EV計算や「経済価値ベースの評価・監督手法の検討に関するフィールドテスト」などでイールドカーブを用いている。
Rでイールドカーブを推定
使用するパッケージ
- YieldCurve (version 4.1):パラメトリックなイールドカーブを生成するパッケージ
- xts (version 0.12.1):高機能な時系列データの型を提供するパッケージ
イールドカーブのデータ
YieldCurveのパッケージにあるFedYieldCurveを用いる。
このデータセットには、1982年1月から2012年12月までの連邦準備制度の金利が含まれています。2012. 金利は、米国財務省証券のコンスタント・マチュリティ(CMT)の市場利回りです。異なる満期(3ヶ月、6ヶ月、1年、2年、3年、5年、7年、10年)で、投資ベースで見積もられたものを月次で収集しています。
Package ‘YieldCurve’ February 19, 2015
データの最初と最後の3か月を見ると、
> require(xts)
> require(YieldCurve)
> data(FedYieldCurve)
> first(FedYieldCurve,'3 month')
R_3M R_6M R_1Y R_2Y R_3Y R_5Y R_7Y R_10Y
1981-12-31 12.92 13.90 14.32 14.57 14.64 14.65 14.67 14.59
1982-01-31 14.28 14.81 14.73 14.82 14.73 14.54 14.46 14.43
1982-02-28 13.31 13.83 13.95 14.19 14.13 13.98 13.93 13.86
> last(FedYieldCurve, '3 month')
R_3M R_6M R_1Y R_2Y R_3Y R_5Y R_7Y R_10Y
2012-09-30 0.10 0.15 0.18 0.28 0.37 0.71 1.15 1.75
2012-10-31 0.09 0.14 0.18 0.27 0.36 0.67 1.08 1.65
2012-11-30 0.07 0.12 0.16 0.26 0.35 0.70 1.13 1.72
この最初と最後の3か月の金利をプロットすると、イールドカーブの形状がかなり異なることがわかる。
> mat.Fed<-c(3/12, 0.5, 1,2,3,5,7,10)
> par(mfrow=c(2,3))
> for( i in c(1,2,3,370,371,372) ){
+ plot(mat.Fed, FedYieldCurve[i,], type="o",
+ xlab="Maturities structure in years", ylab="Interest rates values")
+ title(main=paste("Fed Reserve yield curve at",
+ time(FedYieldCurve[i], sep=" ") ))
+ grid()
+ }
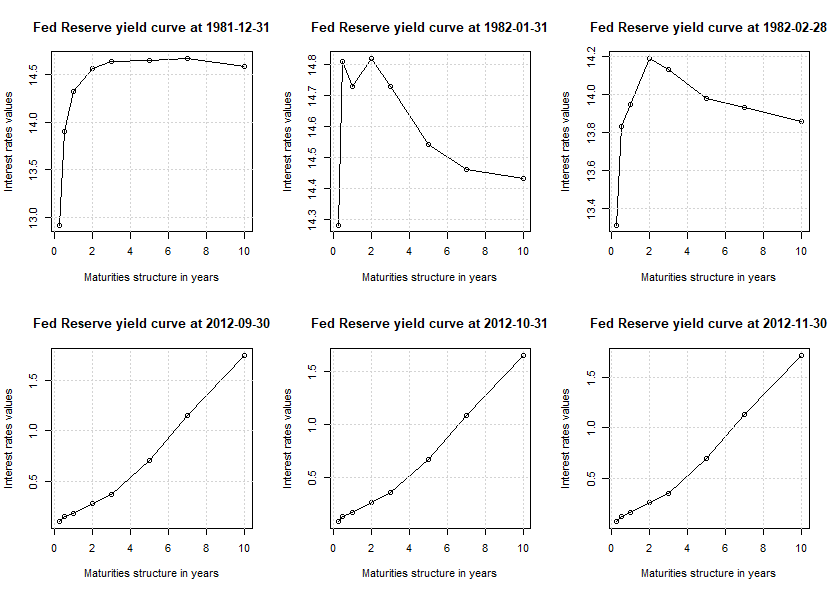
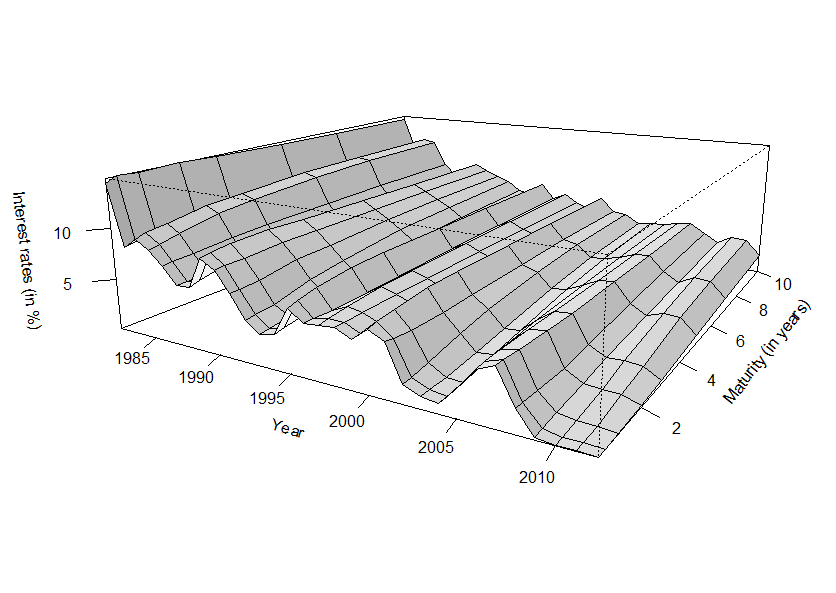
1982年から2012年までのイールドカーブを3Dで表現すると、
> persp(1982:2012, mat.Fed, as.matrix(FedYieldCurve[seq(2,nrow(FedYieldCurve),by=12),]),
+ theta=30,xlab="Year",ylab="Maturity (in years)",
+ zlab="Interest rates (in %)",ticktype = "detailed",shade=.2,expand=.3)
主成分分析
次に、 FedYieldCurve のデータの主成分分析を行う。
主成分分析のサマリーを見ると、最初の3つの主成分で99.9%を説明することができる。
> M <- as.matrix(FedYieldCurve)
> pca.rates <- princomp(M)
> summary(pca.rates)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
Standard deviation 8.5598756 1.16055974 0.2557040238 0.1246520910 5.544781e-02 3.941926e-02 0.0341450611 2.214145e-02
Proportion of Variance 0.9808032 0.01802943 0.0008752298 0.0002079918 4.115435e-05 2.080003e-05 0.0000156064 6.562348e-06
Cumulative Proportion 0.9808032 0.99883266 0.9997078851 0.9999158769 9.999570e-01 9.999778e-01 0.9999934377 1.000000e+00
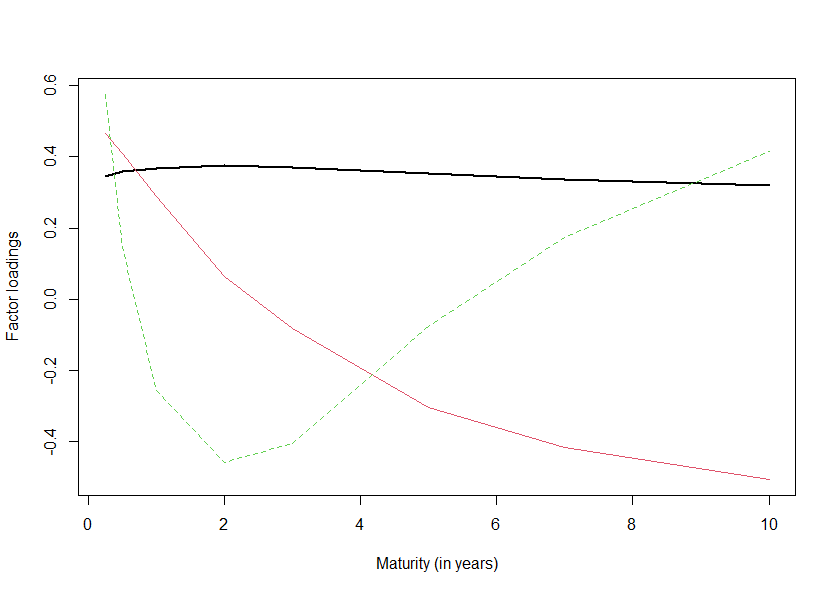
第3主成分までの固有ベクトルを図示すると、
- 第1主成分はフラットであり、イールドカーブの水準を表す
- 第2主成分は単調減少な関数であり、イールドカーブの傾きを表す
- 第3主成分は下に凸の関数であり、イールドカーブの曲率を表す
> factor.loadings <- pca.rates$loadings[,1:3]
> matplot(mat.Fed,factor.loadings,type="l", lwd=c(2,1,1),
+ lty=c(1,1,2),xlab = "Maturity (in years)", ylab = "Factor loadings")
> factor.loadings
Comp.1 Comp.2 Comp.3
R_3M 0.3448377 0.46557527 0.5763589
R_6M 0.3584440 0.41081790 0.1472465
R_1Y 0.3668600 0.28980057 -0.2547488
R_2Y 0.3760976 0.06382216 -0.4586709
R_3Y 0.3703885 -0.08208749 -0.4031082
R_5Y 0.3522393 -0.30238151 -0.0766790
R_7Y 0.3374003 -0.41514327 0.1732862
R_10Y 0.3185436 -0.50585948 0.4152697
ネルソン・シーゲル・モデル
ネルソン・シーゲル・モデルは、イールドカーブの様々な形状や特徴を表現できるような柔軟性のある解析的なモデルである。イールドカーブの最も頻繁に見られる形状は、こぶ状とS字状である。ネルソンとシーゲルは、イールドカーブの典型的な形を生成することができる関数のクラスに注目したモデルを考案した。
$$ y(\tau) = \beta_0 + \beta_1 \Bigg( \frac{1-\exp( -\frac{\tau}{\dot{\lambda}} )}{ \frac{\tau}{\dot{\lambda}} } \Bigg ) + \beta_2 \Bigg( \frac{1-\exp( -\frac{\tau}{\dot{\lambda}} )}{ \frac{\tau}{\dot{\lambda}} } - \exp \Big( \frac{\tau}{\dot{\lambda}} \Big) \Bigg) $$
ここで、
- \( \beta_0\)は、極限まで減衰しない長期的な成分を表す。
- \( \beta_1\)は、\(\tau\)が0に近づくと1に近づき無限大にいくと0に近づく係数を持つので、\( \beta_1\)は短期的な成分を表す。
- \( \beta_2\)は、ゼロから始まって最大になりゼロまで減少するこぶの形の係数を持つので、\( \beta_2\)は中期的な成分と見ることができる。
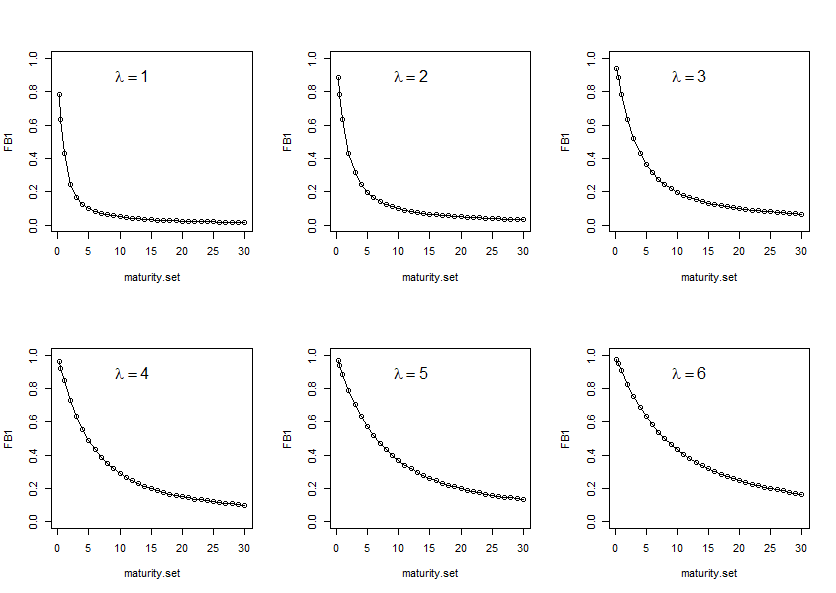
パラメータ\( {\dot{\lambda}}\) 、係数の減衰を制御し、中期的な成分がどの満期で最大になるか、すなわちこぶの位置を決定する。特に, \( {\dot{\lambda}}\) の値が大きいと,係数の減衰が遅くなり,満期が長いほどフィッティングが良くなる。
> factorBeta1 <- function(lambda, Tau)
+ {
+ (1-exp(-Tau/lambda)) / (Tau/lambda)
+ }
> maturity.set<-c(3/12,6/12,seq(1:30))
> lambda.set <- c(0.5,1,2,3,4,5)
> par(mfrow=c(2,3))
> for(i in 1:length(lambda.set)){
+ FB1 <- factorBeta1(lambda.set[i],maturity.set)
+ plot(maturity.set, FB1, type="o", ylim=c(0,1))
+ text(12,0.9, substitute(list(lambda) == group("",list(x),""),list(x=i)),cex=1.5)
+ }
> factorBeta2 <- function(lambda, Tau)
+ {
+ (1-exp(-Tau/lambda)) / (Tau/lambda) - exp(-Tau/lambda)
+ }
> par(mfrow=c(2,3))
> for(i in 1:length(lambda.set)){
+ FB2 <- factorBeta2(lambda.set[i],maturity.set)
+ plot(maturity.set, FB2, type="o", ylim=c(0,0.4))
+ text(i+2,0.35, substitute(list(lambda) == group("",list(x),""),list(x=i)),
+ cex=1.5)
+ abline(v=i, lty=2)
+ }

YieldCurveのパッケージでは、以下の2つの考え方でパラメータの推定を行っている。
- ネルソン・シーゲル・モデルを線形モデルとして推定し、各期間の \( {\dot{\lambda}}\) の値をフィッティング
- 金利カーブの構造に使用される各単一の金利ではなく、ネルソン・シーゲル・モデルのパラメータに基づいて、金利の期間構造を予測
Nelson.Siegelの関数を用いることで、パラメータを推定できる。
> Fed.Rates <- Nelson.Siegel(FedYieldCurve, mat.Fed)
> first(Fed.Rates,'year')
beta_0 beta_1 beta_2 lambda
1981-12-31 14.34594 -1.76249751 3.65006071 0.9999507
1982-01-31 14.14681 0.05426534 2.21914158 0.9999507
1982-02-28 13.61065 -0.54316951 2.70807842 0.9999507
1982-03-31 13.61517 -0.51818755 2.75748648 0.9999507
1982-04-30 13.52630 -1.16619236 2.39279341 0.9999340
1982-05-31 14.13378 -1.43747932 3.23769741 0.9999507
1982-06-30 13.84696 -2.49133196 3.69440615 0.9999507
1982-07-31 13.02162 -4.77732118 4.90917816 0.9999507
1982-08-31 12.10749 -4.77732737 6.11249115 0.9999507
1982-09-30 11.02616 -3.75388964 2.73096552 0.9999340
1982-10-31 10.80609 -2.77592647 0.51759030 0.9999507
1982-11-30 10.84695 -2.96572285 0.05023213 0.9999507
> last(Fed.Rates,'year')
beta_0 beta_1 beta_2 lambda
2011-12-31 5.067016 -5.002900 -5.291108 0.2869276
2012-01-31 5.415061 -5.293744 -5.645563 0.2656801
2012-02-29 5.266186 -5.166166 -5.092655 0.2869276
2012-03-31 5.520023 -5.401772 -5.608334 0.2656801
2012-04-30 6.755632 -6.641670 -6.408147 0.1839190
2012-05-31 5.829454 -5.717205 -5.360561 0.1839190
2012-06-30 5.942878 -5.805087 -5.918784 0.1839190
2012-07-31 6.007142 -5.890642 -5.770203 0.1938867
2012-08-31 6.877328 -6.739946 -6.945611 0.1839190
2012-09-30 6.752246 -6.624800 -6.609233 0.1839190
2012-10-31 6.292996 -6.173300 -6.111852 0.1839190
2012-11-30 6.590762 -6.496260 -6.364102 0.1839190
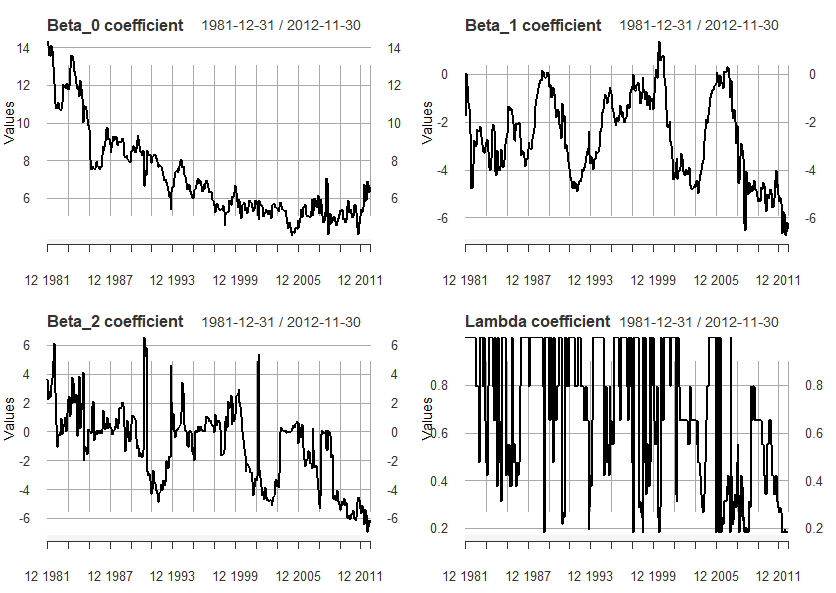
> par(mfrow=c(2,2))
> plot(Fed.Rates$beta_0, main='Beta_0 coefficient', ylab='Values')
> plot(Fed.Rates$beta_1, main='Beta_1 coefficient', ylab='Values')
> plot(Fed.Rates$beta_2, main='Beta_2 coefficient', ylab='Values')
> plot(Fed.Rates$lambda, main='Lambda coefficient', ylab='Values')
推定したパラメータを用いてイールドカーブを計算するには、NSratesの関数を用いる。
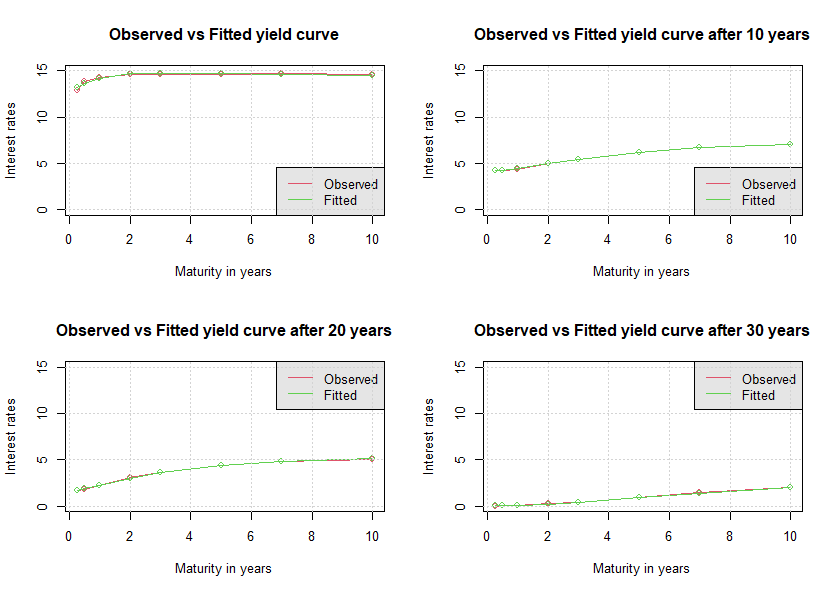
> Fed.yield.curve <- NSrates(Fed.Rates, mat.Fed)
> par(mfrow=c(2,2))
> plot(mat.Fed, as.numeric(FedYieldCurve[1,]), type="o", col=2,
+ ylab="Interest rates", xlab="Maturity in years", ylim=c(0,15))
> lines(mat.Fed, as.numeric(Fed.yield.curve[1,]), type="o", col=3)
> title(main="Observed vs Fitted yield curve")
> legend('bottomright', legend=c("Observed","Fitted"),col=c(2,3), lty=1, bg='gray90')
> grid()
> plot(mat.Fed, as.numeric(FedYieldCurve[120,]), type="o", col=2,
+ ylab="Interest rates", xlab="Maturity in years", ylim=c(0,15))
> lines(mat.Fed, as.numeric(Fed.yield.curve[120,]), type="o", col=3)
> title(main="Observed vs Fitted yield curve after 10 years")
> legend('bottomright', legend=c("Observed","Fitted"),col=c(2,3), lty=1, bg='gray90')
> grid()
> plot(mat.Fed, as.numeric(FedYieldCurve[240,]), type="o", col=2,
+ ylab="Interest rates", xlab="Maturity in years", ylim=c(0,15))
> lines(mat.Fed, as.numeric(Fed.yield.curve[240,]), type="o", col=3)
> title(main="Observed vs Fitted yield curve after 20 years")
> legend('topright', legend=c("Observed","Fitted"),col=c(2,3), lty=1, bg='gray90')
> grid()
> plot(mat.Fed, as.numeric(FedYieldCurve[360,]), type="o", col=2,
+ ylab="Interest rates", xlab="Maturity in years", ylim=c(0,15))
> lines(mat.Fed, as.numeric(Fed.yield.curve[360,]), type="o", col=3)
> title(main="Observed vs Fitted yield curve after 30 years")
> legend('topright', legend=c("Observed","Fitted"),col=c(2,3),
+ lty=1, bg='gray90')
> grid()
スヴェンソン・モデル
ネルソン・シーゲル・モデルは、満期が15年以下の場合に最適なパフォーマンスを発揮し、良い結果を返す。しかしながら、期間構造がより複雑な場合、ネルソン・シーゲル・モデルによるフィッティングはうまくいかない。これは、長期の利回りを引き下げる傾向のある凸性効果のためである。スヴェンソンは、ネルソン・シーゲル・モデルの柔軟性を高め、より複雑な期間構造へのフィッティングを改善することで、ネルソン・シーゲル・モデルを拡張することを提案した。
$$ y(\tau) = \beta_0 + \beta_1 \Bigg( \frac{1-\exp( -\frac{\tau}{\lambda_1} )}{ \frac{\tau}{\lambda_1} } \Bigg ) + \beta_2 \Bigg( \frac{1-\exp( -\frac{\tau}{\lambda_1} )}{ \frac{\tau}{\lambda_1} } - \exp \Big( \frac{\tau}{\lambda_1} \Big) \Bigg) $$
$$ + \beta_3 \Bigg( \frac{1-\exp( -\frac{\tau}{\lambda_2} )}{ \frac{\tau}{\lambda_2} } - \exp \Big( \frac{\tau}{\lambda_2} \Big) \Bigg) $$
YieldCurveのパッケージに入ってある、もう一つのデータ「ECBYieldCurve」を用いてネルソン・シーゲル・モデルに基づくイールドカーブを推定すると、
> data(ECBYieldCurve)
> ECBYieldCurve[5,]
X3M X6M X1Y X2Y X3Y X4Y X5Y X6Y X7Y X8Y X9Y X10Y X11Y X12Y X13Y X14Y
2007-01-04 3.4591 3.6269 3.7766 3.8373 3.84 3.8423 3.8507 3.864 3.8805 3.8985 3.9169 3.9349 3.9521 3.9682 3.9832 3.997
X15Y X16Y X17Y X18Y X19Y X20Y X21Y X22Y X23Y X24Y X25Y X26Y X27Y X28Y X29Y X30Y
2007-01-04 4.0096 4.0212 4.0317 4.0413 4.0501 4.0581 4.0655 4.0723 4.0785 4.0842 4.0895 4.0944 4.099 4.1032 4.1071 4.1108
> maturity.ECB <- c(0.25,0.5,seq(1,30,by=1))
> ECB.Rates <- Nelson.Siegel(ECBYieldCurve[5,], maturity.ECB)
> ECB.yield.curve <- NSrates(ECB.Rates, maturity.ECB)
>
> plot(maturity.ECB, ECB.yield.curve,main="Fitting Nelson Siegel yield curve",
+ xlab=c("Pillars in years"), type="l", col=3)
> lines( maturity.ECB, ECBYieldCurve[5,],col=2)
> legend("topleft",legend=c("fitted yield curve","observed yield curve"),
+ col=c(3,2),lty=1)
> grid()
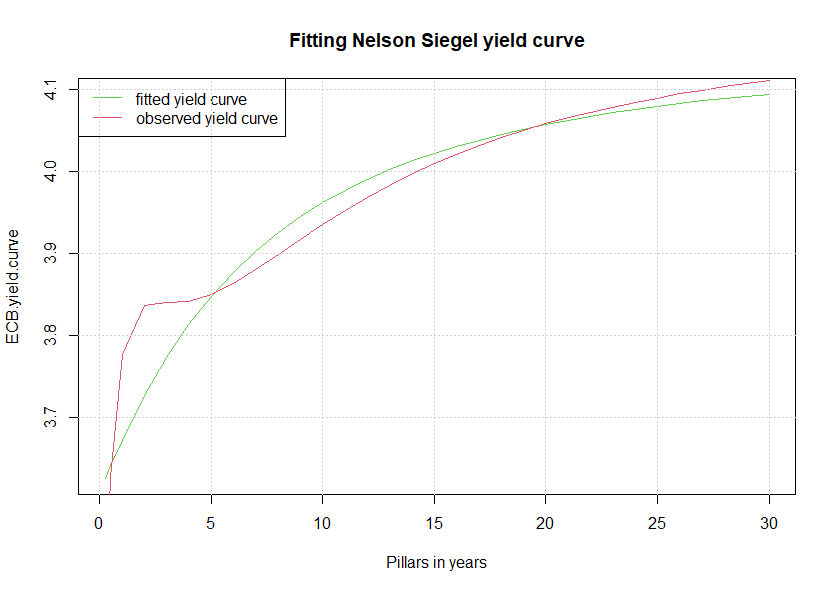
リーマンショック前の2007年ということもあり、ネルソン・シーゲル・モデルでは短期のイールドカーブにあるコブをうまく描写できていない。
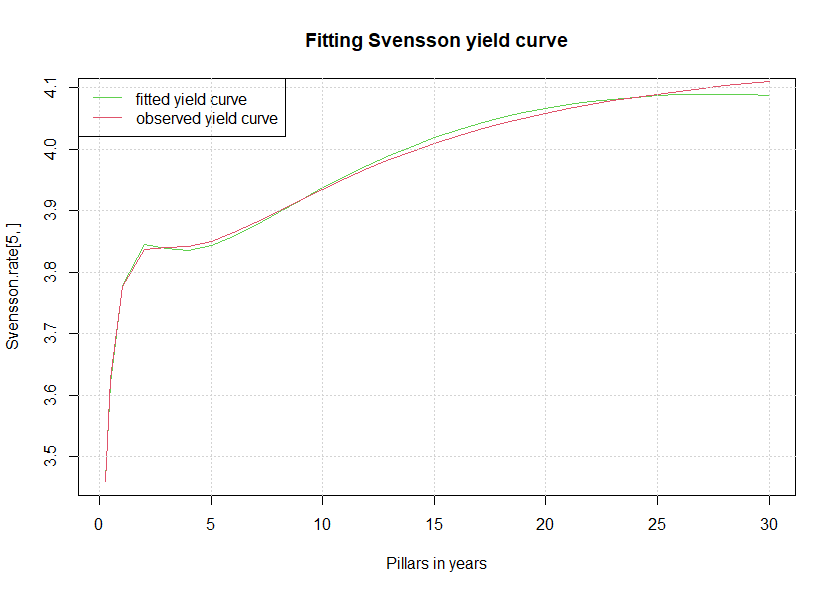
このようなケースでは、スヴェンソン・モデルを用いると、実データへのフィッティングが改善する。
> data(ECBYieldCurve)
> maturity.ECB <- c(0.25,0.5,seq(1,30,by=1))
> A <- Svensson(ECBYieldCurve[1:10,], maturity.ECB )
> Svensson.rate <- Srates( A, maturity.ECB, "Spot" )
> plot(maturity.ECB, Svensson.rate[5,],main="Fitting Svensson yield curve",
+ xlab=c("Pillars in years"), type="l", col=3)
Hit <Return> to see next plot:
> lines( maturity.ECB, ECBYieldCurve[5,],col=2)
> legend("topleft",legend=c("fitted yield curve","observed yield curve"),
+ col=c(3,2),lty=1)
> grid()
(参考文献)
- Charpentier A. Computational Actuarial Science with R. Chapman y Hall/CRC (2014)
- Dickson, D.C.M., Hardy, M.R., Waters, H.R.: Actuarial Mathematics for Life Contingent Risks. Cambridge University, Cambridge (2009)
