因果ダイアグラムを用いた因果探索ができるというベイジアンネットワーク。アクチュアリーであれば線形相関(ピアソンのロー)は知っていると思う。CERAホルダーであれば、スピアマンのローやケンドールのタウなどの順位相関の計算をしたこともあろう。
では、因果とはなにか。
この定義は、アクチュアリー試験にもCERA試験にも登場しない。ベイジアンネットワークの説明に入る前に、因果とはなにかを考えてみたい。
相関と因果
統計検定
日本統計学会公式認定の統計検定3級のテキスト「データの分析」には、以下のような記載がある。
- 2変数間に強い相関があることが因果関係を示すことにはならない。
- 因果関係を示すには、何らかの関係が見られるだけでなく、2変数間に因果を判断できる根拠が必要である。
- 一般に、因果関係があるのではないかと思われる2変数であっても、因果関係を明確に示すことは容易ではない。
このように、因果関係を定義することなく、因果関係の証明の難しさを強調している。
米国アクチュアリー・アカデミー

ビッグデータの活用が進む米国では、アカデミーが「相関と因果」に関する資料(2022年7月)を公表した。この中で、アクチュアリーが実務で遭遇する因果関係の事例として、
- 喫煙と肺癌の関係
- スピードと高速道路の死亡事故の関係
- 台風と屋根の損害の関係
このアカデミーの資料の中に、不思議な表現がある。
It is possible to have causation but not correlation.
同資料の3ページ
「因果関係があるが相関関係がないことがあり得る」というこの一文。続く文章を読むと、その事例として、「水を与えると植物は成長する。でも、水をあげすぎると、成長には逆効果で最終的には植物は枯れる」とある。相関は線形の関係を示すものだが、因果は非線形の関係性を示すこともあるので、これをその事例として扱っているようだ。
統計的因果推論における因果
「統計的因果推論ー回帰分析の新しい枠組みー」(宮川雅巳著)では、反事実モデルによる因果的効果の定義として、「個体がある条件を満たすときとそうでないときの反応の違い」を因果的効果と定義している。でも、このように定義すると、因果的効果は観測されないことになる。例えば、喫煙者である個体が1年以内に死亡した場合、非喫煙者である同一の個体が1年以内に死亡するか否かは観測できないからである。これを、因果推論の基本的問題という。
観測されない因果的効果をいかにして観測するのか。その一つのアプローチが統計的アプローチである。個体で反応の違いをみるのではなく、集団での差の期待値を見ればよいのである。
ここで、筆者が「反事実モデルによる」という枕詞を用いている点が目にとまった。「反事実による因果的効果」があるのであれば、「反事実によらない因果」という概念もあるような気がしたからだ。
用語の定義が不明なときに頼りになる学問、それは哲学である。
現代哲学における因果性
ギリシャ哲学の時代から21世紀まで、因果性の問題は哲学者の気がかりの的であったという。「現代哲学のキーコンセプト 因果性」(ダグラス・クタッチ著)を読んで、因果性がわからず悩んでいるのは自分だけではないと安心した。ソクラテスやプラトンが議論していた命題をすぐに理解できるはずがない。
単称因果と一般因果
宇宙の歴史上で起こる一つ一つの出来事は、固有の時間と場所で生じるので、時空間的な位置に言及することで、どの出来事かを示せる。これを「単称の出来事」とよぶ。例えば、特定の時間に特定の場所でおきた交通事故は「単称の出来事」の一つだ。この事故の部分的な原因とみなせる単称の出来事(例えば、特定の急ブレーキ)のことを「原因」とよぶ。このような関係を単称因果という。「特定の急ブレーキが特定の交通事故の原因だった」というように、単称因果は過去時制で表現されることが多い。
一方、一般因果は、「急ブレーキは交通事故の原因になる」というように、現在時制で表現されることが多い。
単称因果と一般因果の違いを直感的に理解するために、幸運なアクチュアリー受験生に注目してみよう。
業務多忙で前日まで十分な勉強ができずに数学の試験を迎えた彼は、前日に、山を張って2001年度の過去問の解答を丸暗記した。翌日、試験会場で数学の問題を見ると、幸運にも2001年度の過去問と類似した問題が半分以上あった。そのお陰もあって、彼は数学の試験に合格したという。
「2001年度の過去問の丸暗記」は、試験合格の単称因果だが、一般因果ではないことは明らかであろう。
線形因果と非線形因果
原因が強くなるとそれに比例して結果も大きくなる因果関係を線形因果とよぶ。
Aさんは「2016年度~2020年度の過去問を丸暗記」した。5年分の過去問に不安を感じたAさんは、さらに「2001年度~2015年度の過去問を丸暗記」した。Aさんは無事アクチュアリー試験に合格することができた。平等主義的な意味で因果を探しているなら、5年の過去問の丸暗記も15年の過去問の丸暗記も同等の原因である。でも、結果を予測したり説明したりすることが目的なら、勉強量の違いによって原因の相対的な強さを示せばよい。つまり、15年の過去問の丸暗記は5年のそれよりも3倍強い原因である。このような因果関係を線形因果とよぶ。
非線形因果の典型例は、何らかのしきい値を超えることによって結果が生み出されるケースである。
Bさんは「昭和37年度からの過去問すべてを丸暗記」した。でも、Bさんの暗記力のキャパシティは20年分が限界だったので、記憶力のキャパオーバーで試験は不合格だった(やや無理がある設定だがご勘弁を)。「すべての過去問を丸暗記しようとしたことが原因で不合格だった」とは言えそうだ。では、特定の一年の過去問の丸暗記が不合格の部分的原因だったと言えるだろうか。
米国アクチュアリー・アカデミーの「水を与えると植物は成長する。でも、水をあげすぎると、成長には逆効果で最終的には植物は枯れる」という例示は、2つの意味での因果を含んでいる。前段の「水を与えると植物は成長する」という関係性は線形因果、後段は植物が水を吸収できるしきい値を超えたことで植物が枯れるという関係性を示しているので、非線形因果の事例であることがわかる。相関は、線形もしくはモノトニックな関係性を図る尺度なので、非線形な因果関係を捉えることはできない。
産出的因果と差異形成的因果
少し無理がある設定だが、再びアクチュアリー試験を題材に、この違いを説明したい。
Aさんは過去問を分析し、50点獲得できる公式集を作成した。Bさんは予知能力があり、出題問題の半分を予知できる。AさんとBさんは協力しなくても、60点の合格点は確保できる学力を有する。一方、協力すると、科目別優秀賞を獲得でき、一人10万円を受領できる。合計20万円を、10万円ずつ配分するのは公平か否か。
- Aさんの主張「Bさんが半分の賞金を得るのは公平ではない。Bさんは何も努力せず、予知した出題問題を教えただけなんだから」
- Bさんの主張「でも、僕の予知問題がなければ、君は優秀賞を獲得できなかっただろ。僕の予知問題を使ったことこそが、優秀賞か否かの違いをもたらしたんだ」
- Aさんの反論「それはお互い様でしょ。私の公式集がなければ、お互い優秀賞を獲得できなかったんだから」
ここで、協力によって生まれた余剰の公平な分配方法をめぐり、対立する2つの意見が示されている。Aさんは、労働力に比例して余剰を分配するという立場。Bさんは、成果の差異に応じて余剰を分配するという立場。どちらの意見が公平だろうか?
Bさんの差異形成の立場を推す人は、以下のケースもあわせて考えてほしい。
Aさんは過去問を分析し、75点獲得できる公式集を作成した。Bさんも同様に、25点獲得できる公式集を作成した。AさんとBさんは協力しなくても、60点の合格点は確保できる学力を有する。一方、協力すると、科目別優秀賞を獲得でき、一人10万円を受領できる。合計20万円を、10万円ずつ配分するのは公平か否か。
ここで、AさんはBさんの3倍努力し、科目別優秀賞の獲得に貢献している。この場合、Aさんは賞金合計の3/4をもらうべき、と考える人が多いと思う。これは、産出的因果の考え方に基づく。
因果の確率上昇説
因果とは何かを記していくと、長くなりすぎるので、ここで一気に確率上昇説まで飛躍する。アクチュアリーの世界でも、決定論的なシミュレーションと確率論的なシミュレーションがあるように、因果にも、「決定性説」と「確率上昇説」が存在する。
因果論の歴史を振り返ると、
「原因とは、結果を何らかの意味で必然化する単称の出来事である」
という考え方にとらわれてきた。
でも、アクチュアリーが取り扱うリスクには不確実性を伴う。例えば、喫煙はがんの原因である、という言い方は一般のアクチュアリーに受け入れられるだろう。これは確率論的な主張であって、喫煙することで、しない場合よりも、がん罹患率が高まるということであって、喫煙すると必ずがんになるというわけではない。
この確率上昇説のメリットは、統計データを用いて因果関係を実験で示すことができる点にある。一方、デメリットとしては、
- 原因と結果の非対称性が示しにくい
- 擬似相関を因果関係と誤認しやすい
- シンプソンのパラドックスの取り扱い
などの問題が多数指摘されている。
ベイジアンネットワークに基づく因果モデル構築論の起点にある「確率上昇説」は、因果を語る上での一つの仮説であり、いくつかの課題がある点を念頭において、ベイジアンネットワークの理解を深めていきたい。
Rでベイジアンネットワーク
ベイジアンネットワークの矢印は、因果関係を何ら仮定していない点が因果ダイアグラムと異なる。この矢印は、単に順確率であることを表しており、ベイズの定理は、この方向を逆転させる方法(事前確率に尤度比を乗ずる)を教えてくれる。
使用するパッケージ
- bnlearn(version4.7.1):Bayesian Network Learningの略。ベイジアンネットワークの学習と推論のパッケージ。
- gRain(version1.3.10):gRaphical model inferenceの略。厳密推論を行うためのパッケージ。
有向非循環グラフ(DAG:Directed Acyclic Graphs)
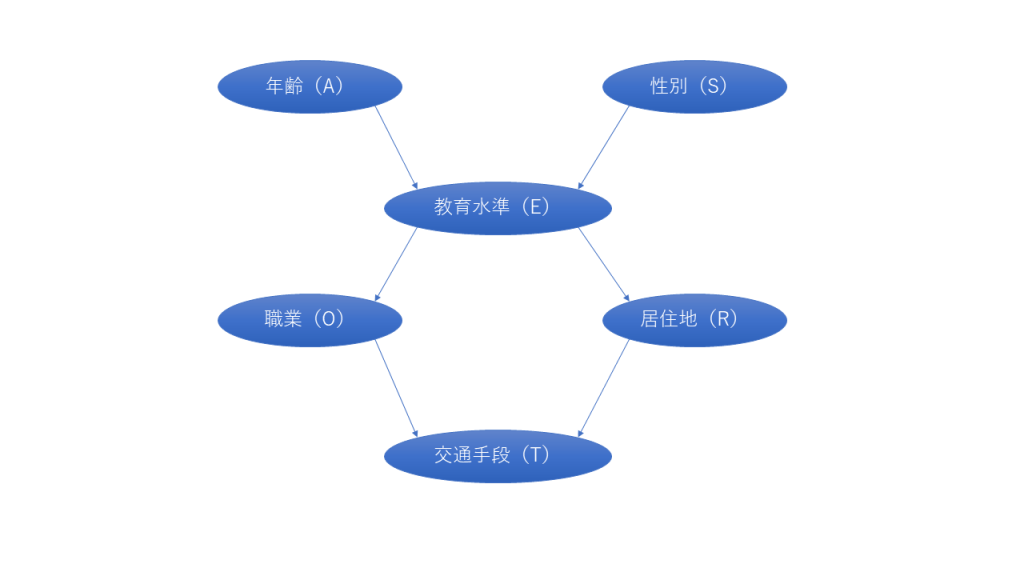
有向非循環グラフ(DAG)とは、循環していない、変数間の関係を矢印の向きで示したグラフのこと。グラフは、ノードとアークで構成される。
- ノード:上記のDAGの場合、年齢、性別、教育水準、職業、居住地、交通手段がノード。ノードのことを変数と呼ぶこともある。
- アーク:ノード間の直接的な依存関係を表す矢印。
- 親ノード:アークの尾にあたるノード。例えば、年齢は教育水準の親ノード。
- 子ノード:アークの先頭にあたるノード。例えば、職業は教育水準の子ノード。
ノードとアークのないDAGは、以下の関数で構築できる。
empty.graph(nodes, num = 1)
交通手段の調査に関するDAGを構築するには、empty.graphでノードを定義し、アークに対応する行列を割りあてればよい。
> dag <- empty.graph(nodes = c("A", "S", "E", "O", "R", "T"))
> arc.set <- matrix(c("A", "E",
+ "S", "E",
+ "E", "O",
+ "E", "R",
+ "O", "T",
+ "R", "T"),
+ byrow = TRUE, ncol = 2,
+ dimnames = list(NULL, c("from", "to")))
> arcs(dag) <- arc.set
> dag
Random/Generated Bayesian network
model:
[A][S][E|A:S][O|E][R|E][T|O:R]
nodes: 6
arcs: 6
undirected arcs: 0
directed arcs: 6
average markov blanket size: 2.67
average neighbourhood size: 2.00
average branching factor: 1.00
generation algorithm: Empty
ここで、modelの部分は、このグラフ構造を条件付き確率の積で表現したものであり、以下の積と対応する。この式の左辺を大局的分布、右辺を局所的分布と呼ぶ。
$$ Pr(A,S,E,O,R,T) = Pr(A)Pr(S)Pr(E|A,S)Pr(O|E)Pr(R|E)Pr(T|O,R) $$
次に、ノードのレベルを付与して、確率を定義するために以下の関数を用いる。
custom.fit(x, dist, ordinal, debug = FALSE)
この関数を用いると、DAGと局所的分布を含むリスト(条件付き確率表を意味するcptオブジェクト)を結合し、bnオブジェクトを作成することができる。
> A.lv <- c("young", "adult", "old")
> S.lv <- c("M", "F")
> E.lv <- c("high", "uni")
> O.lv <- c("emp", "self")
> R.lv <- c("small", "big")
> T.lv <- c("car", "train", "other")
> A.prob <- array(c(0.30, 0.50, 0.20), dim = 3, dimnames = list(A = A.lv))
> A.prob
A
young adult old
0.3 0.5 0.2
> S.prob <- array(c(0.60, 0.40), dim = 2, dimnames = list(S = S.lv))
> S.prob
S
M F
0.6 0.4
> O.prob <- array(c(0.96, 0.04, 0.92, 0.08), dim = c(2, 2),
+ dimnames = list(O = O.lv, E = E.lv))
> O.prob
E
O high uni
emp 0.96 0.92
self 0.04 0.08
> R.prob <- array(c(0.25, 0.75, 0.20, 0.80), dim = c(2, 2),
+ dimnames = list(R = R.lv, E = E.lv))
> R.prob
E
R high uni
small 0.25 0.2
big 0.75 0.8
> R.prob <- matrix(c(0.25, 0.75, 0.20, 0.80), ncol = 2,
+ dimnames = list(R = R.lv, E = E.lv))
>
> E.prob <- array(c(0.75, 0.25, 0.72, 0.28, 0.88, 0.12, 0.64, 0.36, 0.70,
+ 0.30, 0.90, 0.10), dim = c(2, 3, 2),
+ dimnames = list(E = E.lv, A = A.lv, S = S.lv))
>
> T.prob <- array(c(0.48, 0.42, 0.10, 0.56, 0.36, 0.08, 0.58, 0.24, 0.18,
+ 0.70, 0.21, 0.09), dim = c(3, 2, 2),
+ dimnames = list(T = T.lv, O = O.lv, R = R.lv))
>
> cpt <- list(A = A.prob, S = S.prob, E = E.prob, O = O.prob, R = R.prob,
+ T = T.prob)
> bn <- custom.fit(dag, cpt)
ベイジアンネットワークのパラメータ数は、大局的分布に比べると、局所的分布の方が少ない。
大局的分布の場合、年齢は3通り、性別は2通り、教育水準は2通り、職業は2通り、居住地は2通り、交通手段は3通りなので、すべての組み合わせは3×2×2×2×2×3=144通りとなる。確率は合計すると1なので、パラメータ数は144から1を減じた143となる。
一方で、局所的分布で見ると、Pr(A)の自由なパラメータは2通り。
| 青年 | 中年 | 高齢者 |
| 0.30 | 0.50 | 0.20 |
Pr(S)の自由なパラメータは1通り。
| 男性 | 女性 |
| 0.60 | 0.40 |
Pr(E|A,S)の自由なパラメータは6通り。
| 高校卒業 | 大学卒業 | |
| 青年かつ男性 | 0.75 | 0.25 |
| 中年かつ男性 | 0.72 | 0.28 |
| 高齢者かつ男性 | 0.88 | 0.12 |
| 青年かつ女性 | 0.64 | 0.36 |
| 中年かつ女性 | 0.70 | 0.30 |
| 高齢者かつ女性 | 0.90 | 0.10 |
Pr(O|E)の自由なパラメータは2通り。
| 従業員 | 自営業 | |
| 高校卒業 | 0.96 | 0.04 |
| 大学卒業 | 0.92 | 0.08 |
Pr(R|E)の自由なパラメータは2通り。
| 小規模 | 大規模 | |
| 高校卒業 | 0.25 | 0.75 |
| 大学卒業 | 0.20 | 0.80 |
Pr(T|O,R)の自由なパラメータは8通り。
| 自動車 | 電車 | その他 | |
| 小規模かつ従業員 | 0.48 | 0.42 | 0.10 |
| 小規模かつ自営業 | 0.56 | 0.36 | 0.08 |
| 大規模かつ従業員 | 0.58 | 0.24 | 0.18 |
| 大規模かつ自営業 | 0.70 | 0.21 | 0.09 |
すべての自由なパラメータを合計すると21通りとなる。
> nparams(bn)
[1] 21
> arcs(bn)
from to
[1,] "A" "E"
[2,] "S" "E"
[3,] "E" "O"
[4,] "E" "R"
[5,] "O" "T"
[6,] "R" "T"
> bn$R
Parameters of node R (multinomial distribution)
Conditional probability table:
E
R high uni
small 0.25 0.20
big 0.75 0.80
> R.cpt <- coef(bn$R)
> R.cpt
E
R high uni
small 0.25 0.20
big 0.75 0.80
ベイジアンネットワークのパラメータの推定
データ
Bayesian Networks with Examples in Rの第1章のSurvey dataを用いる。
> survey <- read.table("survey.txt", header = TRUE, colClasses = "factor")
> head(survey)
A R E O S T
1 adult big high emp F car
2 adult small uni emp M car
3 adult big uni emp F train
4 adult big high emp M car
5 adult big high emp M car
6 adult small high emp F train
>> dim(survey)
[1] 500 6
最尤推定
bn.fit(x, data, cluster, method, ..., keep.fitted = TRUE, debug = FALSE)
Available methods for discrete Bayesian networks are:
mle: the maximum likelihood estimator for conditional probabilities.
bayes: the classic Bayesian posterior estimator with a uniform prior matching that in the Bayesian Dirichlet equivalent (bde) score.
hdir: the hierarchical Dirichlet posterior estimator for related data sets from Azzimonti, Corani and Zaffalon (2019).
bn.fitにDAG構造とデータをわたして、methodでmleを選択すると、最尤推定に基づくパラメータ(局所的分布の確率)を求めることができる。
最尤推定したパラメータは、クロス集計して計算した確率と一致していることがわかる。
> bn.mle <- bn.fit(dag, data = survey, method = "mle")
> table(survey[, c("O", "E")])
E
O high uni
emp 358 125
self 7 10
> prop.table(table(survey[, c("O", "E")]), margin = 2)
E
O high uni
emp 0.98082192 0.92592593
self 0.01917808 0.07407407
> bn.mle$O
Parameters of node O (multinomial distribution)
Conditional probability table:
E
O high uni
emp 0.98082192 0.92592593
self 0.01917808 0.07407407
ベイズ推定
bn.fit(x, data, cluster, method, ..., keep.fitted = TRUE, debug = FALSE)
Available methods for discrete Bayesian networks are:
mle: the maximum likelihood estimator for conditional probabilities.
bayes: the classic Bayesian posterior estimator with a uniform prior matching that in the Bayesian Dirichlet equivalent (bde) score.
hdir: the hierarchical Dirichlet posterior estimator for related data sets from Azzimonti, Corani and Zaffalon (2019).
iss: a numeric value, the imaginary sample size used by the bayes method to estimate the conditional probability tables associated with discrete node
bn.fitのmethodでbayesを選択するとベイズ推定を行うことができる。これは、条件付き確率表に関する一様事前分布から事後確率を算出するアプローチである。issの値が小さければ経験的頻度に近い値となる。以下の事例でiss=10000とした結果からもわかるように、issの値が大きくすると、経験的頻度に関する情報が薄れていき、一様分布に収束する。
> bn.bayes <- bn.fit(dag, data = survey, method = "bayes", iss = 1)
> bn.bayes$O
Parameters of node O (multinomial distribution)
Conditional probability table:
E
O high uni
emp 0.98016416 0.92435424
self 0.01983584 0.07564576
> bn.bayes <- bn.fit(dag, data = survey, method = "bayes", iss = 10)
> bn.bayes$O
Parameters of node O (multinomial distribution)
Conditional probability table:
E
O high uni
emp 0.97432432 0.91071429
self 0.02567568 0.08928571
> bn.bayes <- bn.fit(dag, data = survey, method = "bayes", iss = 10000)
> bn.bayes$O
Parameters of node O (multinomial distribution)
Conditional probability table:
E
O high uni
emp 0.5327120 0.5111977
self 0.4672880 0.4888023
DAG構造の学習:検定とスコア
条件付き独立性検定
アークは、ノード間の確率的な依存関係を意味する。条件付き独立性検定はデータをもとに、確率的な依存関係を支持するか否かを評価する目的で用いる。
例えば、以下のDAGに教育水準(E)から交通手段(T)へのアークを加えるかどうかを考える。
帰無仮説:TとEが{O、R}の条件付きで確率的に独立
対立仮説:TとEが{O、R}の条件付きで確率的に独立ではない

条件付き独立性検定は、bnlearnのci.test関数を用いる。
ci.test(x, y, z, data, test, B, debug = FALSE)
相互情報量(mutual information): an information-theoretic distance measure. It's proportional to the log-likelihood ratio (they differ by a 2n factor) and is related to the deviance of the tested models. The asymptotic chi-square test (mi and mi-adf, with adjusted degrees of freedom), the Monte Carlo permutation test (mc-mi), the sequential Monte Carlo permutation test (smc-mi), and the semiparametric test (sp-mi) are implemented.
shrinkage estimator for the mutual information (mi-sh): an improved asymptotic chi-square test based on the James-Stein estimator for the mutual information.
ピアソンのカイ二乗検定(Pearson's X^2: the classical Pearson's X^2 test) for contingency tables. The asymptotic chi-square test (x2 and x2-adf, with adjusted degrees of freedom), the Monte Carlo permutation test (mc-x2), the sequential Monte Carlo permutation test (smc-x2) and semiparametric test (sp-x2) are implemented.
> ci.test("T", "E", c("O", "R"), test = "mi", data = survey)
Mutual Information (disc.)
data: T ~ E | O + R
mi = 9.8836, df = 8, p-value = 0.2733
alternative hypothesis: true value is greater than 0
> ci.test("T", "E", c("O", "R"), test = "x2", data = survey)
Pearson's X^2
data: T ~ E | O + R
x2 = 8.2375, df = 8, p-value = 0.4106
alternative hypothesis: true value is greater than 0
いずれの検定においても、p値は5%以上であり、教育水準(E)と交通手段(T)の依存関係に有意差があるとは言えない。
bnlearnのarc.strength関数を用いると、各アークに対して依存関係の有意性に関する検定を行うことができる。
arc.strength(x, data, criterion = NULL, ..., debug = FALSE)
If criterion is a conditional independence test, the strength is a p-value (so the lower the value, the stronger the relationship). The conditional independence test would be that to drop the arc from the network.
以下のように、職業(O)から交通手段(T)には依存関係がないことが確認できる。
> arc.strength(dag, data = survey, criterion = "x2")
from to strength
1 A E 0.0009777168
2 S E 0.0012537013
3 E O 0.0026379469
4 E R 0.0005599201
5 O T 0.4339127237
6 R T 0.0013584250
ネットワークスコア
ネットワークスコアは、ベイジアンネットワーク全体としてのDAGが、データの依存構造をどの程度よく反映しているのかを図る指標。
bnlearnのscore関数を用いるとBICを計算できる。ここで、score関数を用いて計算されるBICは、通常のBICの式にマイナスがかけられている。したがって、BICの数値が高いほど適合度は良いことになる。
score(x, data, type = NULL, ..., by.node = FALSE, debug = FALSE)
AIC and BIC are computed as logLik(x) - k * nparams(x), that is, the classic definition rescaled by -2. Therefore higher values are better, and for large sample sizes BIC converges to log(BDe).
以下にBICの結果と、BDe(Bayesian Dirichlet equivalent uniform)のスコアを示す。ユーザーが事前にネットワーク構造を書くのは難しいし、誤っている可能性も高いので、現実的にはBDeを用いることが望ましい。BDeのスコアに用いるissは、事前分布(一様分布)に割り振る重みとしての役割を果たす。
> set.seed(456)
> score(dag, data = survey, type = "bic")
[1] -2012.687
> score(dag, data = survey, type = "bde", iss = 10)
[1] -1998.284
random.graph関数を用いて生成したDAGに比べると、上記のBICの方が高く、適合度は良いことがわかる。
> rnd <- random.graph(nodes = c("A", "S", "E", "O", "R", "T"))
> modelstring(rnd)
[1] "[A][S|A][E|A:S][O|S:E][R|S:E][T|S:E]"
> score(rnd, data = survey, type = "bic")
[1] -2034.991
ネットワークのスコアが最大となるDAGを探索するためのアルゴリズムも存在する。単純なアルゴリズムとして、山登り法(hill-climbing)がある。これは、アークなしのDAGからスタートし、アークを加減することで、スコアの増減を探索する方法である。以下のように、bnlearnのhc関数にデータをわたすだけで実行できる。
> learned <- hc(survey)
> modelstring(learned)
[1] "[R][E|R][T|R][A|E][O|E][S|E]"
> score(learned, data = survey, type = "bic")
[1] -1998.432
BICスコアが最大のDAGを図示すると以下のようになる。事前知識にもとづくDAGとは大きくことなる。この結果は、surveyデータをもとに、すべての依存関係を正確に学習できないことを示唆している。
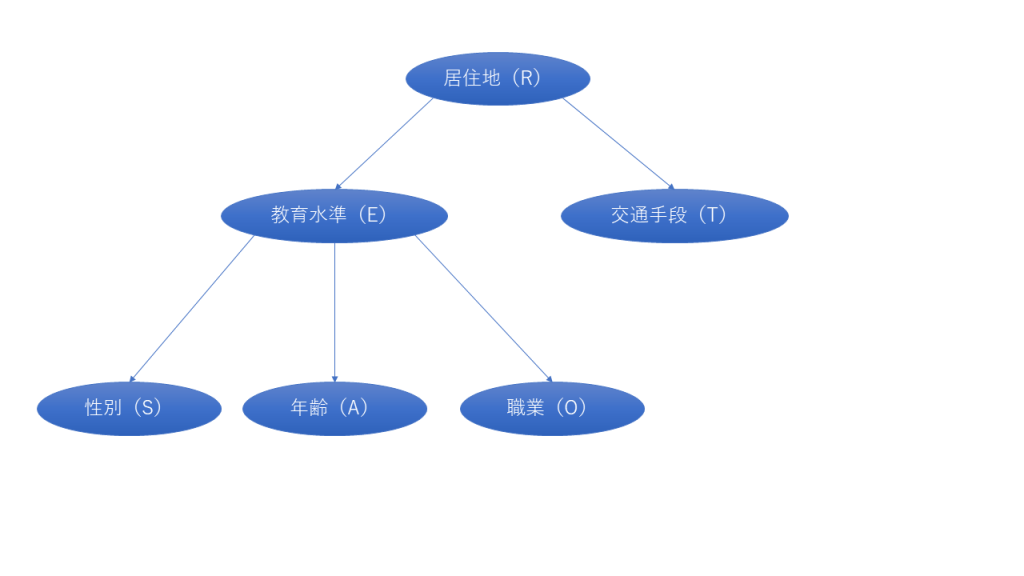
arc.strength関数で、アークを取り除くことで変化するBICを計算することができる。山登り法で決定したDAGはBICが最大のDAGなので、いずれのアークを除去してもBICは下がる。
> arc.strength(learned, data = survey, criterion = "bic")
from to strength
1 R E -3.3896261
2 E S -2.7260640
3 R T -1.8484171
4 E A -1.7195441
5 E O -0.8266937
一方、事前知識にもとづいて作成したDAGは、職業(O)から交通手段(T)のアークを除去することでBICが著しく増加することがわかる。この結果は、条件付独立性検定のp値の値とも整合的である。
> arc.strength(dag, data = survey, criterion = "bic")
from to strength
1 A E 2.4889383
2 S E 1.4824183
3 E O -0.8266937
4 E R -3.3896261
5 O T 10.0457874
6 R T 2.9734338
DAG構造を用いた推論
cを所与としたときにaとbが条件付き独立であることの定義を確認すると、
$$ p(a|b,c) = p(a|c) $$
これは、以下のように書くこともできる。
$$ p(a,b|c) = p(a|b,c) p(b|c) = p(a|c)p(b|c) $$

性別(S)と居住地(R)には、教育水準(E)を経由したパスが存在する。したがって、性別(S)と居住地(R)は何らかの関連性を持つ。しかしながら、教育水準(E)を固定すると、性別(S)と居住地(R)は条件付き独立となる。これをd分離(有向分離)と呼ぶ。dnlearnのdsep関数を用いてd分離を調べることができる。
> path.exists(dag, from = "S", to = "R")
[1] TRUE
> dsep(dag, x = "S", y = "R")
[1] FALSE
> dsep(dag, x = "S", y = "R", z = "E")
[1] TRUE
$$ p(S,E,R) = p(S)p(E|S)p(R|E) $$
教育水準(E)に関する情報があると、性別(S)と居住地(R)は条件付き独立となる(最後の等式はベイズの定理を利用)。このような構造を連結結合(serial connections)と呼ぶ。
$$ p(S,R|E) = \frac{p(S,R,E)}{p(E)} = \frac{p(S)p(E|S)p(R|E)}{p(E)} = p(S|E)p(R|E)$$
次に、職業(O)と居住地(R)は、いずれも教育水準(E)の影響を受けている。
> dsep(dag, x = "O", y = "R")
[1] FALSE
> dsep(dag, x = "O", y = "R", z = "E")
[1] TRUE
教育水準(E)に関する情報があると、職業(O)と居住地(R)は条件付き独立となる。2つのアークが中心のノードから分岐するような形になっていることから、このような構造を分岐結合(divergent connections)と呼ぶ。
$$ p(O,R|E) = \frac{p(O,R,E)}{p(E)} = \frac{p(E)p(O|E)p(R|E)}{p(E)} = p(O|E)p(R|E)$$
最後に、年齢(A)と性別(S)は、教育水準(E)で合流する形になっている。
> dsep(dag, x = "A", y = "S")
[1] TRUE
> dsep(dag, x = "A", y = "S", z = "E")
[1] FALSE
このケースでは、もともと独立だった年齢(A)と性別(S)が、教育水準(E)に関する情報があると、年齢(A)と性別(S)は条件付き独立ではなくなる。このような構造を収束結合(convergent connections)と呼ぶ。
$$ p(A,S|E) = \frac{p(A,S,E)}{p(E)} = \frac{p(A)p(S)p(E|A,S)}{p(E)} \neq p(A|E)p(S|E)$$
厳密推論
bnlearnのas.grain関数を用いてgrainオブジェクトに変換し、コンパイルすると確率表が計算できる。
> junction <- compile(as.grain(bn))
例えば、「女性と交通手段の関係」を調査する場合、男女全体と女性だけの比較をすると、あまり大差がないことがわかる。確率の計算には、gRainのquerygrain関数を用いる。setEvidence関数を用いて、エビデンス(この場合は女性)をgrainオブジェクトに入力することができる。
> querygrain(junction, nodes = "T")$T
T
car train other
0.5618340 0.2808573 0.1573088
> jsex <- setEvidence(junction, nodes = "S", states = "F")
> querygrain(jsex, nodes = "T")$T
T
car train other
0.5620577 0.2806144 0.1573280
次に、「居住地と交通手段の関係」を調査してみる。以下のように、小規模都市の場合、自動車が少なく、電車が多い。
> jres <- setEvidence(junction, nodes = "R", states = "small")
> querygrain(jres, nodes = "T")$T
T
car train other
0.48388675 0.41708494 0.09902831
querygrain関数のtypeでconditionalを指定すると、setEvidenceで指定したエビデンス(ここでは、教育水準(E))で条件付けられた確率を計算することができる。この結果をみると、男女とも、条件付確率は同じ値となる。これは、教育水準(E)で条件つけられた場合、性別(S)と交通手段(T)は独立であることを意味している。つまり、教育水準を知っていれば、性別を知ったところで交通手段の好みを知るための有益な情報にはならないことを示唆している。
> jedu <- setEvidence(junction, nodes = "E", states = "high")
> querygrain(jedu, nodes = c("S", "T"), type = "conditional")
T
S car train other
M 0.612557 0.612557 0.612557
F 0.387443 0.387443 0.387443
実際、dsep関数を用いて、性別(S)と交通手段(T)は教育水準(E)でd分離されている。
> dsep(bn, x = "S", y = "T", z = "E")
[1] TRUE
ピアソンのカイ二乗検定を用いて、性別(S)と交通手段(T)の独立性を検定することもできる。
> SxT.cpt <- querygrain(jedu, nodes = c("S", "T"), type = "joint")
> SxT.cpt
T
S car train other
M 0.3426644 0.1736599 0.09623271
F 0.2167356 0.1098401 0.06086729
> SxT.ct = SxT.cpt * nrow(survey)
> chisq.test(SxT.ct)
Pearson's Chi-squared test
data: SxT.ct
X-squared = 2.2783e-30, df = 2, p-value = 1
近似推論
近似推論とは、棄却サンプリングや尤度重み付き法などを用いたモンテカルロ・シミュレーションのことである。bnlearnのcpquery関数やcpdist関数で実行できる。
棄却サンプリング法の結果は以下の通り。引数nを大きくすることで、近似精度は高まるが、計算に時間がかかる。
> cpquery(bn, event = (S == "M") & (T == "car"), evidence = (E == "high"))
[1] 0.3385472
> cpquery(bn, event = (S == "M") & (T == "car"),
+ evidence = (E == "high"), n = 10^6)
[1] 0.3420785
棄却サンプリング法よりも良い近似理論の方法として、尤度重み付き法がある。これは、cpquery関数でmethodをlwと指定することで可能となる。
> cpquery(bn, event = (S == "M") & (T == "car"),
+ evidence = list(E = "high"), method = "lw")
[1] 0.3488647
cpdist関数を用いると、エビデンスに適合するような変数のランダム観測値を算出し、それらの観測値を含んだデータフレームを返してくれる。このデータフレームを用いて確率表を計算しておくと、「教育水準が高い人の中で、最も多い性別と交通手段の組み合わせは?」という質問に対して、「自動車を運転する男性」というような回答を導くことができる。
> SxT <- cpdist(bn, nodes = c("S", "T"), evidence = (E == "high"))
> head(SxT)
S T
1 F car
2 M car
3 M car
4 M train
5 M other
6 F car
> prop.table(table(SxT))
T
S car train other
M 0.34338495 0.17332247 0.09263787
F 0.21570225 0.11274110 0.06221136
(参考文献)
- Rと事例で学ぶベイジアンネットワーク
- Pattern Recognition and Machine Learning
- 現代哲学のキーコンセプト 因果性
