イントロダクション
ベクトル
Rでの最もシンプルなオブジェクトはベクトルであろう。ベクトルを表す c( ) 関数は concatenate もしくは combine の略とされる。
> x <- c(-2,0,1)
> x
[1] -2 0 1
> y <- c(0, 2^x)
> y
[1] 0.00 0.25 1.00 2.00
NULLのオブジェクトは以下のようなループ処理で役立つ。
> set.seed(1)
> u <- runif(10)
> u
[1] 0.266 0.372 0.573 0.908 0.202 0.898 0.945 0.661 0.629 0.062
>
> x <- NULL
> for(i in 1:10){ x <- c(x, max(u[1:i]))}
> x
[1] 0.27 0.37 0.57 0.91 0.91 0.91 0.94 0.94 0.94 0.94
seq( ) や rep( ) を用いてベクトルを作成することもできる
> seq(from=0, to=10, by=2)
[1] 0 2 4 6 8 10
> seq(from=0, to=10, length=6)
[1] 0 2 4 6 8 10
> rep(c(1,2,3), times = 3)
[1] 1 2 3 1 2 3 1 2 3
> rep(c(1,2,3), each = 3)
[1] 1 1 1 2 2 2 3 3 3
ベクトルの並べ替えは sort( ) を用いて行う。
> x <- c(1,2,3)
> sort(x, decreasing=TRUE)
[1] 3 2 1
ベクトルに名前を付与するには、
> names(x) <- c("Apple", "Banana", "Carrot")
> x
Apple Banana Carrot
1 2 3
ベクトルの一部にアクセスする方法は、いくつか存在する。
> x[c(2,3)]
Banana Carrot
2 3
> x[c("Banana", "Carrot")]
Banana Carrot
2 3
>
> set.seed(1)
> u <- runif(10)
> u
[1] 0.266 0.372 0.573 0.908 0.202 0.898 0.945 0.661 0.629 0.062
> u[u>0.9]
[1] 0.91 0.94
> which(u>0.9)
[1] 4 7
値の比較には == を用いるが、以下の点に留意が必要であり、all.equal( ) を用いる方が無難である。
> z = seq(1,5,1)
> z
[1] 1 2 3 4 5
> z == 3
[1] FALSE FALSE TRUE FALSE FALSE
> 4/10 - 2/10
[1] 0.2
> 6/10 - 4/10
[1] 0.2
> 4/10 - 2/10 == 6/10 - 4/10
[1] FALSE
> all.equal((4/10 - 2/10), (6/10 - 4/10))
[1] TRUE
> sqrt(3)^2 == 3
[1] FALSE
> all.equal(sqrt(3)^2, 3)
[1] TRUE
行列
行列は複数のベクトルを持つオブジェクトである。以下のように、行列と行列の掛け算は行列とベクトルの掛け算よりも時間を要する。
> m <- 10
> X <- matrix(seq(1, m), nrow=2, ncol=5)
> X
[,1] [,2] [,3] [,4] [,5]
[1,] 1 3 5 7 9
[2,] 2 4 6 8 10
> n <- 1000
> A <- matrix(seq(1, n^2), n, n)
> B <- matrix(seq(1, n^2), n, n)
> C <- 1:n
> system.time((A%*%B)%*%C)
ユーザ システム 経過
0.74 0.00 0.75
> system.time(A%*%(B%*%C))
ユーザ システム 経過
0.02 0.00 0.02
データの読み込み
Rはメモリを使うので、サイズの大きなデータの処理には向いていない。でも、ff や bigmemory のパッケージを用いると、大規模データを処理できる。また、rpy2 や PypeR を用いると、Python から R を利用できる。zip形式のデータを読み込むと早くなることもある。
ファイルをread.tableで読み込むとデータフレームとなる。以下のように、データフレームをdata.tableにすると、処理速度が速くなる。
> library(data.table)
> n <- 10000
> df <- data.frame(matrix(rnorm(n^2), n, n))
> df$index <- 1:nrow(df)
> dt <- data.table(df)
> system.time(df[df$X1>1, ])
ユーザ システム 経過
0.5 3.0 27.4
> system.time(dt[dt$X1>1, ])
ユーザ システム 経過
0.38 2.62 16.11
生保数理
使用するライブラリ
- lifecontingencies (version 1.3.7)
- markovchain (version 0.8.6)
金利の計算
利率を i とした場合、割引率は \( d = \frac{i}{1+i} \) と定義される。interest2Discount を用いると、実利率 i から割引率 d に変換することができる。
> library(lifecontingencies)
>
> i <- 0.05
> d <- i/(1+i)
> 100 * (1+i)^2
[1] 110.25
> 110.25 * (1-d)^2
[1] 100
>
> d
[1] 0.04761905
> interest2Discount(i = 0.05)
[1] 0.04761905
> 110.25 * (1- interest2Discount(i = 0.05)) ^2
[1] 100
Function
- interest2Discount: 実利率を割引率に変換
- discount2Interest: 割引率を実利率に変換
- interest2Intensity: 実利率を利力に変換
- intensity2Interest: 利力を実利率に変換
転化回数(1年間に利息を元金に繰り入れる回数)を k とした場合、名称利率 \( i^{(k)} \)と実利率 i には次の関係式が成り立つ。
$$ (1 + \frac{i^{(k)}}{k}) ^k = 1+i $$
同様に、 名称割引率 \( d^{(k)} \)と実割引率 d には次の関係式が成り立つ。
$$ (1 - \frac{d^{(k)}}{k}) ^k = 1-d $$
例えば、転化回数が2回、名称利率 6% の場合、実利率および実割引率を計算すると、
> nominal2Real(i=0.06, k=2)
[1] 0.0609
> nominal2Real(i=0.06, k=2, type='discount')
[1] 0.0591
Function
- nominal2Real: 名称利率を実利率に変換
- real2Nominal: 実利率を名称利率に変換
転化回数が2回、名称利率 6% の場合 、1年後の100の支払の現在価値は以下のように計算できる。ここで、presentValue の引数の probabilities で1を指定しているのは、この支払は確率100%で行われるからである。
> annualDiscount = nominal2Real(i=0.06, k=2, type="discount")
> i = discount2Interest(annualDiscount)
> presentValue(cashFlows = 100, timeIds=1, interestRates=i, probabilities=1)
[1] 94.09
Function
- presentValue: キャッシュフローの現在価値を計算
この presentValue の関数を用いると、NPV(Net Present Value: 正味現在価値)を計算することもできる。
$$ NPV = \sum_{j=1}^K CF_j(1+i_j)^{-t_j} $$
NPVは生命保険のProfit Measureの一つで、生命保険の収益をキャッシュフローとみなし、リスク割引率で割り引くことで計算される。EPVFP(Expected Present Value of Future Profit)と呼ばれることもある。
例えば、今500万円の投資を行い、1年後に100万円、2年後に200万円、3年後に300万円、4年後に250万円を受け取るキャッシュフローのNPVは、
> cfs = c(-500,100,200,300,250)
> times = 0:4
> NPV = presentValue(cashFlows = cfs, t=times, i = 0.05)
> NPV
[1] 241.4709
$$ \sum_{t=0}^n CF_j(1+i)^{-t} = 0$$
を満たす実利率を内部収益率と呼ぶ。上記の取引の内部収益率は、
> f <- function(irr) (presentValue(cashFlows=CF, timeIds=TI, interestRate=irr))^2
> CF = cfs
> TI = times
> IRR = nlm(f, 0.01)$estimate
> IRR
[1] 0.2147816
NPVを二乗した関数を定義し、それを最小化する値をニュートン法で用いることで内部収益率を計算している。最適化がうまくいっていることは、以下のように、21.478%の利率を用いると、このキャッシュフローの現在価値は0となっていることで確認できる。
> presentValue(cashFlows=cfs, t=times, i=IRR)
[1] 0.0005410981
次に、年金現価率を計算するには、annuity の関数を用いる。期初払い(due)と期末払い(immediate)は type で指定する。
> annuity(i=0.05, n=5, type="due")
[1] 4.545951
> annuity(i=0.05, n=5, type="immediate")
[1] 4.329477
ここで、期初払いのn年確定年金の現価率は、
$$ 1 + v + v^2 + ... + v^{n-1} $$
ここで、期末払いのn年確定年金の現価率は、
$$ v + v^2 + ... + v^{n} $$
Function
- annuity: 確定年金の現価率を計算
- accumulatedValue: 確定年金の終価率を計算
永久年金の現価率は、引数 n を Inf で指定することで求まる。
> annuity(i=0.05, n=Inf, type="due")
[1] 21
> annuity(i=0.05, n=Inf, type="immediate")
[1] 20
年金終価率の計算には accumulatedValue の関数を用いる。
> accumulatedValue(i=0.05, n=5, type="due")
[1] 5.801913
> accumulatedValue(i=0.05, n=5, type="immediate")
[1] 5.525631
据置年金の計算も、同じ annuity の関数で引数 m を指定することで計算できる。
> annuity(i=0.05, n=10, m=2, type="due")
[1] 7.354033
> annuity(i=0.05, n=10, m=1, type="immediate")
[1] 7.354033
年 k 回払いの年金現価率を計算するには、引数 k を指定する。
> annuity(i=0.05, n=10, k=2, type="due")
[1] 8.010123
> annuity(i=0.05, n=10, k=2, type="immediate")
[1] 7.817079
年金現価率を用いると、元利均等返済の返済額も計算することができる。100万円を年実利率5%で毎月返済する場合、1年間で元利均等返済するには、
> L <- 1000000
> R <- L/annuity(i=0.05, n=1, k=12, type="immediate")/12
> instalments <- rep(R,12)
> balance <- numeric(12)
> balance[1] <- L*(1+0.05)^(1/12)-R
> for(i in 2:12) balance[i] <- balance[i-1] * (1+0.05)^(1/12) - R
> amortization <- data.frame(month=1:12, rate=round(R,0), balance = round(balance,0))
> amortization
month rate balance
1 1 85557 918518
2 2 85557 836703
3 3 85557 754555
4 4 85557 672073
5 5 85557 589254
6 6 85557 506098
7 7 85557 422604
8 8 85557 338769
9 9 85557 254593
10 10 85557 170073
11 11 85557 85209
12 12 85557 0
lifecontingenciesには、デュレーションやコンベクシティを計算するための関数も用意されている。
> CFs = c(3,3,3,3,103)
> TIs = seq(1,5,1)
> bondPrice = presentValue(cashFlows = CFs, timeIds=TIs, interestRates=0.05)
> duration(cashFlows = CFs, timeIds=TIs, i=0.05, macaulay=TRUE)
[1] 4.701744
> convexity(cashFlows = CFs, timeIds=TIs, i=0.05)
[1] 25.05967
Function
- duration: キャッシュフローのデュレーションを計算
- convexity: キャッシュフローのコンベクシティを計算
生命表
次に、死亡率から生命表を作成してみたい。利用するのは、日本版死亡データベースの全国データ。ウェブサイトからread.csvでデータを読み込んで、2019年男性の死亡率をprobs2lifetableの引数に入れると、生命表が作成できる。ここで、typeを"qx"と指定しているが、"px"とすると生存率に基づいて生命表を作成することもできる。
> jmd_qx <- read.csv('http://www.ipss.go.jp/p-toukei/JMD/00/STATS/Mx_1x1.txt',
+ skip = 1, sep = "")
> jmd_qx2019 <- hmd_qx[hmd_qx$Year == 2019,]
> lifetable_2019m <- probs2lifetable(probs = as.numeric(jmd_qx2019$Male),
+ radix = 100000,
+ type = "qx",
+ name = "JMD 2019 male")
> summary(lifetable_2019m)
This is lifetable: JMD 2019 male
Omega age is: 111
Expected curtated lifetime at birth is: 80.67133
Function
- probs2lifetable: 生存率/死亡率から生命表を作成
summaryを見ると、最終年齢(Omega age)は111歳、略算平均余命は80.67歳であることがわかる。ここで、略算平均余命は、
$$ e_x = \sum_{t=1}^{\omega - x} \, _t p _x $$
であるので、この式に基づいて略算平均余命を計算してみると、
> sum(lifetable_2019m@lx[lifetable_2019m@x%in%(1:110)]/lifetable_2019m@lx[lifetable_2019m@x==0])
[1] 80.67133
これは、exnの関数を用いて、
> exn(lifetable_2019m, type = "curtate")
[1] 80.67133
と計算することもできる。このtypeを"complete"に変更することで、完全平均余命も計算できる。
> exn(lifetable_2019m, type = "complete")
[1] 81.17133
$$ 完全平均余命=\int_{t=0}^{\infty} \, _t p_x dt $$
死亡率を計算する関数としてqxがあり、例えば、65歳の人が20年以内に死亡する確率は以下のようにすれば求まる。
> (lifetable_2019m@lx[lifetable_2019m@x==65] -
+ lifetable_2019m@lx[lifetable_2019m@x==85])/lifetable_2019m@lx[lifetable_2019m@x==65]
[1] 0.4757416
> qxt(lifetable_2019m, 65, 20)
[1] 0.4757416
同様に、pxtを用いると、65歳の人が20年生存する確率が求まる。
> pxt(lifetable_2019m, 65, 20)
[1] 0.5242584
Function
- pxt: 生命表から生存率を計算
- qxt: 生命表から死亡率を計算
- mxt: 生命表から中央死亡率を計算
- exn: 生命表から平均余命を計算
連生の場合の生存確率の計算にはpxyzt、平均余命の計算にはexyztを用いる。連生の計算を行うために、まず日本版死亡データベースから2019年女性の死亡率を取り込んだ上で、その生命表を作成し、男女の生命表をリストを作る。そのうえで、pxyztおよびexyztの引数でそのリストを指定し、各年齢と期間、そしてstatusで共存(joint)か最終生存者(last)を指定することで、連生の生存確率および平均余命の計算ができる。
> jmd_qx2019 <- hmd_qx[hmd_qx$Year == 2019,]
> lifetable_2019f <- probs2lifetable(probs = as.numeric(jmd_qx2019$Female),
+ radix = 100000,
+ type = "qx",
+ name = "JMD 2019 female")
> tables <- list(male=lifetable_2019m, female=lifetable_2019f)
>
> pxyzt(tablesList = tables, x=c(65,60), t=20, status="joint")
[1] 0.4458616
> pxyzt(tablesList=tables, x=c(65,60), t=20, status="last")
[1] 0.9288583
> exyzt(tablesList = tables, x=c(65,60), t=20, status="joint")
[1] 15.32771
Function
- pxyzt: 複数の生命表から連生の生存率を計算
- qxyzt: 複数の生命表から連生の死亡率を計算
- exyzt: 複数の生命表から連生の平均余命を計算
保険料の計算
保険料の計算は以下のステップで行われる。
- 金融および人口統計学上の前提条件(将来のキャッシュフローを割引くための金利や生存確率を推定するための生命表)などを定義
- 生存確率や死亡確率と関連するキャッシュフローの数理計算上の現在価値(契約上約束された給付の実際の価格と最終的な費用・利益)を決定
- 一時払いか分割払いかを考慮して保険料を決定
まず、計算基数のデータフレームを作る。ここで、金利は2.0%と仮定している。
> act_2019m <- new("actuarialtable",
+ x=lifetable_2019m@x,
+ lx=lifetable_2019m@lx,
+ interest=0.02)
> df_act_2019m <- as(act_2019m, "data.frame")
> head(df_act_2019m)
x lx Dx Nx Cx Mx Rx
1 0 100000.00 100000.00 4043429 191.666667 20717.07 1592488
2 1 99804.50 97847.55 3943429 27.819401 20525.40 1571771
3 2 99775.56 95901.15 3845582 15.325380 20497.58 1551246
4 3 99759.29 94005.41 3749681 12.810541 20482.26 1530748
5 4 99745.43 92149.36 3655675 9.485963 20469.45 1510266
6 5 99734.95 90333.02 3563526 7.793437 20459.96 1489796
Function
- new("actuarialtable"): 計算基数表を作成
- 計算基数表はS4オブジェクト
ここで、
$$ D_x = v^x l_x $$
$$ C_x = v^{x+1} d_x $$
$$ N_x = \sum_{t=0}^{\omega - x} D_{x+t} $$
$$ M_x = \sum_{t=0}^{\omega - x} C_{x+t} $$
この計算基数を用いて、40歳加入、男性、10年定期保険の一時払い保険料を計算基数を用いて計算すると、
$$ 定期保険の一時払い保険料(計算基数バージョン) = \frac{M_x - M_{x+n}}{D_x} $$
> 1000000 * with(df_act_2019m, (Mx[41] - Mx[51])/Dx[41])
[1] 12839.3
これを、定期保険の定義式に基づいて計算すると、
$$ 定期保険の一時払い保険料(定義式)= \sum_{t=1}^n v^t \, _{t-1|} q_x$$
> (probhealth <- -diff(df_act_2019m$lx)[df_act_2019m$x%in%40:49]/
+ df_act_2019m$lx[df_act_2019m$x==40])
[1] 0.000964000 0.001001034 0.001057917 0.001216312 0.001283536 0.001445970 0.001576934 0.001822293 0.001966399
[10] 0.002183729
> disc <- (1+0.02)^(-(1:10))
> sum(disc*probhealth) * 1000000
[1] 12839.3
また、Axnを用いると、引数に生命表、年齢、保障期間を指定することで、一時払い保険料の計算ができる。
> P <- 1000000 * Axn(actuarialtable=act_2019m, x=40, n=10)
> P
[1] 12839.3
同様に、60歳支給開始期初払い終身年金現価率を、計算基数および axn を用いて計算すると、
> with(df_act_2019m, Nx[61]/Dx[61])
[1] 18.87915
> axn(actuarialtable = act_2019m, x=60)
[1] 18.87915
ここで、
$$ 期初払い終身年金現価率 = \sum_{t=0}^{\omega - x} v^t \, _t p_x = \frac{N_x}{D_x} $$
60歳支給開始期末払い終身年金現価には、据置期間を指定する引数 m を用いる。
> axn(actuarialtable = act_2019m, x=60, m=1)
[1] 17.87915
Function
- Axn: 定期保険/終身保険の価値を評価
- axn: 生命年金の価値を評価
- Exn: 生存保険の価値を評価
- AExn: 養老保険の価値を評価
- Axyzn: 連生保険の価値を評価
- axyzn: 連生年金の価値を評価
責任準備金の計算
責任準備金は、給付現価から収入現価を控除して計算するので、
> P <- Axn(act_2019m, 60) / axn(act_2019m,60)
> V <- Axn(act_2019m, 60+10) - P * axn(act_2019m,60+10)
> V
[1] 0.2802023
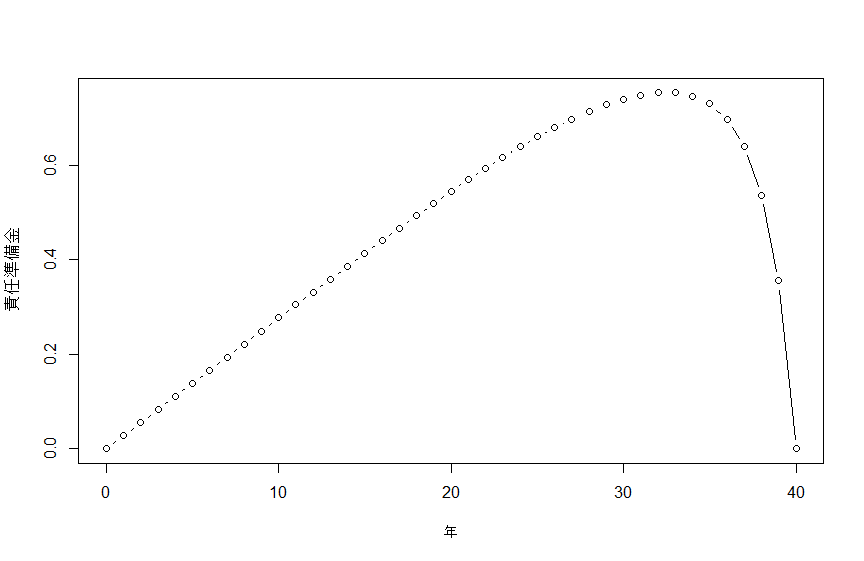
責任準備金のカーブは以下のような関数を定義することで描くことができる。
> P <- Axn(act_2019m, 60,40) / axn(act_2019m, 60,40)
> V <- function(t) Axn(act_2019m, 60+t, 40-t) - P * axn(act_2019m, 60+t, 40-t)
> VecT <- seq(0,40)
> plot(VecT, Vectorize(V)(VecT), type="b", xlab="年", ylab="責任準備金")
シミュレーション
ここまで決定論的な手法の説明を行ってきたが、Life Contingenciesには確率論的な計算を行う関数も用意されている。
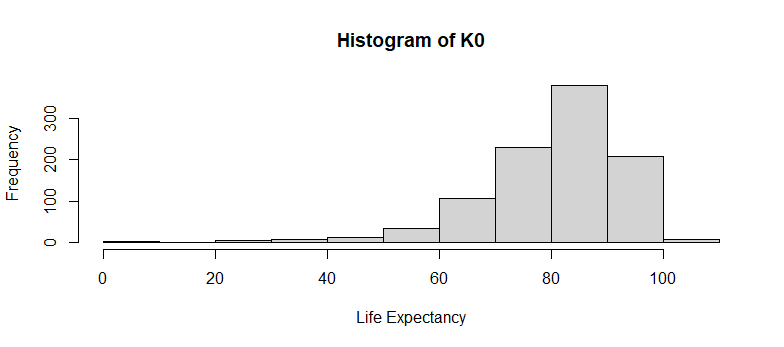
> K0 <- rLife(n=10^3, object=act_2019m, x=0, type="Kx")
> hist(K0, xlab="Life Expectancy")
> exn(act_2019m)
[1] 80.67133
> mean(K0)
[1] 80.771
> t.test(x=K0, mu=exn((act_2019m)))
One Sample t-test
data: K0
t = 0.24009, df = 999, p-value = 0.8103
alternative hypothesis: true mean is not equal to 80.67133
95 percent confidence interval:
79.9564 81.5856
sample estimates:
mean of x
80.771
Function
- rLife: 生命表を用いて、ある年齢からの余命の乱数を生成
- rLifexyz: 生命表を用いて、連生に関する余命の乱数を生成
一時払い保険料についても、rLifeContingenciesを用いてシミュレーションすることができる。シミュレーションした結果を用いてパーセンタイル方式の保険料を計算すると、
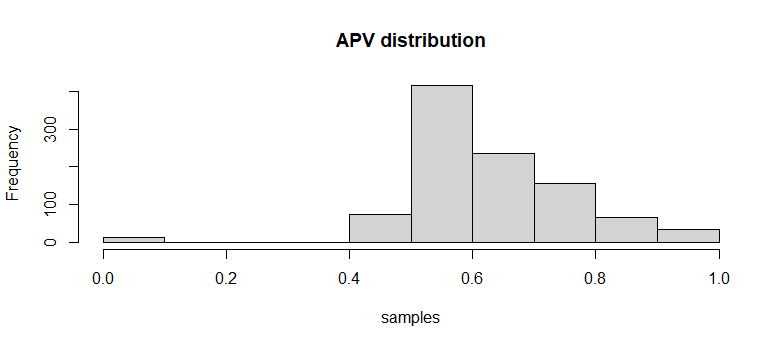
> samples <- rLifeContingencies(n=10^3, lifecontingency = "Axn", object=act_2019m, x=60, t= 40, parallel=TRUE)
> hist(samples, main="APV distribution")
> APV <- Axn(act_2019m, x=60, n=40)
> percentilePremium <- quantile(x=samples, p=0.95)
> APV
[1] 0.624371
> percentilePremium
95%
0.8534904
Function
- rLifeContingencies: 保険や年金の現価の乱数を生成
マルコフ連鎖
マルコフ連鎖とは、
$$ P(X_{n+t}|X_1 = x_1, X_2=x_2, ... , X_n = x_n) = P(X_{n+1} | X_n = x_n) $$
Q0~Q4の4つのマルコフ連鎖のオブジェクトを作成し、それをリスト化する。ここで、HはHealthy、IはIllness、DはDeathを表す。
> stateNames <- c("H","I","D")
> Q0 <- new("markovchain",
+ states=stateNames,
+ transitionMatrix=matrix(c(0.7, 0.2, 0.1,0.1, 0.6, 0.3,0, 0, 1),
+ byrow=TRUE, nrow=3))
> Q1 <- new("markovchain",
+ states=stateNames,
+ transitionMatrix=matrix(c(0.5, 0.3, 0.2,0, 0.4, 0.6,0, 0, 1),
+ byrow=TRUE, nrow=3))
> Q2 <- new("markovchain",
+ states=stateNames,
+ transitionMatrix=matrix(c(0.3, 0.2, 0.5,0, 0.2, 0.8,0, 0, 1),
+ byrow=TRUE,nrow=3))
> Q3 <- new("markovchain",
+ states=stateNames,
+ transitionMatrix=matrix(c(0, 0, 1,0, 0, 1,0, 0, 1),
+ byrow=TRUE, nrow=3))
> Qlist<-new("markovchainList",
+ markovchains=list(Q0,Q0,Q0,Q1,Q1,Q1,Q2,Q2,Q2,Q3))
>
> Q1
Unnamed Markov chain
A 3 - dimensional discrete Markov Chain defined by the following states:
H, I, D
The transition matrix (by rows) is defined as follows:
H I D
H 0.5 0.3 0.2
I 0.0 0.4 0.6
D 0.0 0.0 1.0
このQ1を用いて、Healthyな人が2年後にDeathする確率は、
> transitionProbability(Q1^2, "H", "I")
[1] 0.27
これをプロットすると、
plot(Q1)

ここで定義したマルコフ連鎖のリストを用いて弱体者年金の年金現価を計算してみたい。予定利率は2%とする。年1回期央払いの10年終身年金であり、推移確率はQlistで定義される。Healthyの人には100を、Illnessになると200の年金額を支給する。この年金現価を計算する関数をgetAPVで定義すると、
> i<-0.02
> v<-(1+i)^-1
> getAPV<-function(mcList,t1="H"){
+ lifeStates<-character()
+ t2<-markovchainSequence(n=1,markovchain=mcList@markovchains[[1]],t0=t1) #state during second year
+ t3<-markovchainSequence(n=1,markovchain=mcList@markovchains[[2]],t0=t2) #state during third year
+ t4<-markovchainSequence(n=1,markovchain=mcList@markovchains[[3]],t0=t3) #state during fourth year
+ t5<-markovchainSequence(n=1,markovchain=mcList@markovchains[[4]],t0=t4) #state during fifth year
+ t6<-markovchainSequence(n=1,markovchain=mcList@markovchains[[5]],t0=t5) #state during sixth year
+ t7<-markovchainSequence(n=1,markovchain=mcList@markovchains[[6]],t0=t6) #state during seventh year
+ t8<-markovchainSequence(n=1,markovchain=mcList@markovchains[[7]],t0=t7) #state during eighth year
+ t9<-markovchainSequence(n=1,markovchain=mcList@markovchains[[8]],t0=t8) #state during ninth year
+ t10<-markovchainSequence(n=1,markovchain=mcList@markovchains[[9]],t0=t9) #state during tenth year
+ t11<-markovchainSequence(n=1,markovchain=mcList@markovchains[[10]],t0=t10) #state during eleventh year
+ lifeStates<-c(t1,t2,t3,t4,t5,t6,t7,t8,t9,t10)
+ APV<-0
+ for(i in 1:11){
+ value<-ifelse(lifeStates[i]=="H",100, ifelse(lifeStates[i]=="I",200,0))*v^((i-0.5))
+ APV<-APV+value
+ if(lifeStates[i]=="D") break}
+ return(APV)}
>
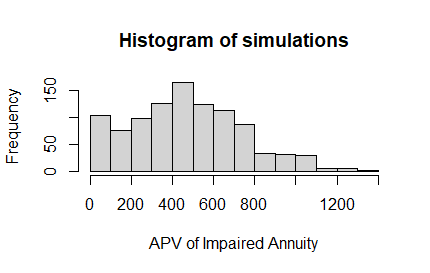
> simulations<-numeric(1000)
> set.seed(1)
> for(i in 1:1000) simulations[i]<-getAPV(Qlist)
> mean(simulations)
[1] 493.9891
このシミュレーションのヒストグラムは、
Function
- transitionProbability: 推移確率を計算
- markovchainSequence: 推移行列をもとにマルコフ連鎖の状態のシークエンスを作成
(参考文献)
- Charpentier A. Computational Actuarial Science with R. Chapman y Hall/CRC (2014)
